Units

The mole is a quantity of substance. The new prefix ‘guaca’ is defined such that one guacamole equals Avocado’s Number.

—G. Byrne.

For better or worse, there are a variety of unit systems that engineers have to contend with on a regular basis.

The two systems we will deal with most commonly are the following:

unit system

selected base units

SI (International System of Units)

\(\si{m}\), \(\si{kg}\), \(\si{N}\), \(\si{s}\)

United States customary

\(\si{ft}\), \(\si{lb_{m}}\), \(\si{lb_{f}}\), \(\si{s}\)

What is a pound?

Some sources use the term pound to mean pound mass (lbm or \(\si{lb_{m}}\)) and others use it to mean pound force (lbf or \(\si{lb_{f}}\)). This is analogous to the difference between mass and weight, which are also commonly confused.

Weight is the force exerted on a mass by the local gravitational field, \(f = m \cdot a = m \cdot g\), where \(\si{g}\) is the acceleration of gravity. Thus, \(\si{lb_{f}}\) = \(\si{lb_{m}}\) \(\cdot\) \(\si{g}\).

What is a gmol?… a kgmol?… a lbmol?

First, what is a mole?

A mole is a certain number of molecules, atoms, electrons, etc. In the SI system, the mole has about \(\num{6.022140d23}\) particles. This is correctly defined as a gram mole, though SI units officially designate this as a mole.

Alternatively, a \(\si{kgmol}\) (kilogram mole) is equal to \(1000\) gram moles, and therefore can be thought of as having \(1000\) times \(\num{6.022140d23}\) particles.

Recall that there are approximately 454 grams per \(\si{lb_{m}}\), so a \(\si{lbmol}\) (pound mole) has \(454\) times \(\num{6.022140d23}\) particles and is therefore larger than a \(\si{gmol}\).

Another way to look at the mole unit is as a conversion factor between number of moles and mass, using the molecular weight (\(MW\)).

Keep in mind that the value for the \(MW\) is the same across these various mole units.

For instance, for carbon

\(MW\) = 12.0 \(\si{g}\) / \(\si{gmol}\) = 12.0 \(\si{kg}\) / \(\si{kgmol}\) = 12.0 \(\si{lb_{m}}\) / \(\si{lbmol}\)

In summary

\(\si{gmol}\) = (mass in grams) / \(MW\)

\(\si{kgmol}\) = (mass in kilograms) / \(MW\)

\(\si{lbmol}\) = (mass in pounds) / \(MW\)

or

mass in \(\si{g}\) = \(MW\) \(\cdot\) \(\si{gmol}\)

mass in \(\si{kg}\) = \(MW\) \(\cdot\) \(\si{kgmol}\)

mass in \(\si{lb_{m}}\) = \(MW\) \(\cdot\) \(\si{lbmol}\)

Converting between units

Converting units is a very important skill for CBEs.

It helps us to

  • use a consistent set of units in calculations

  • transfer results into and out of other unit systems of interest

  • assure that equations are formulated correctly

Your textbook, Introduction to Chemical Engineering: Tools for Today and Tomorrow has tables of common conversion factors (page xix of the 5th edition):

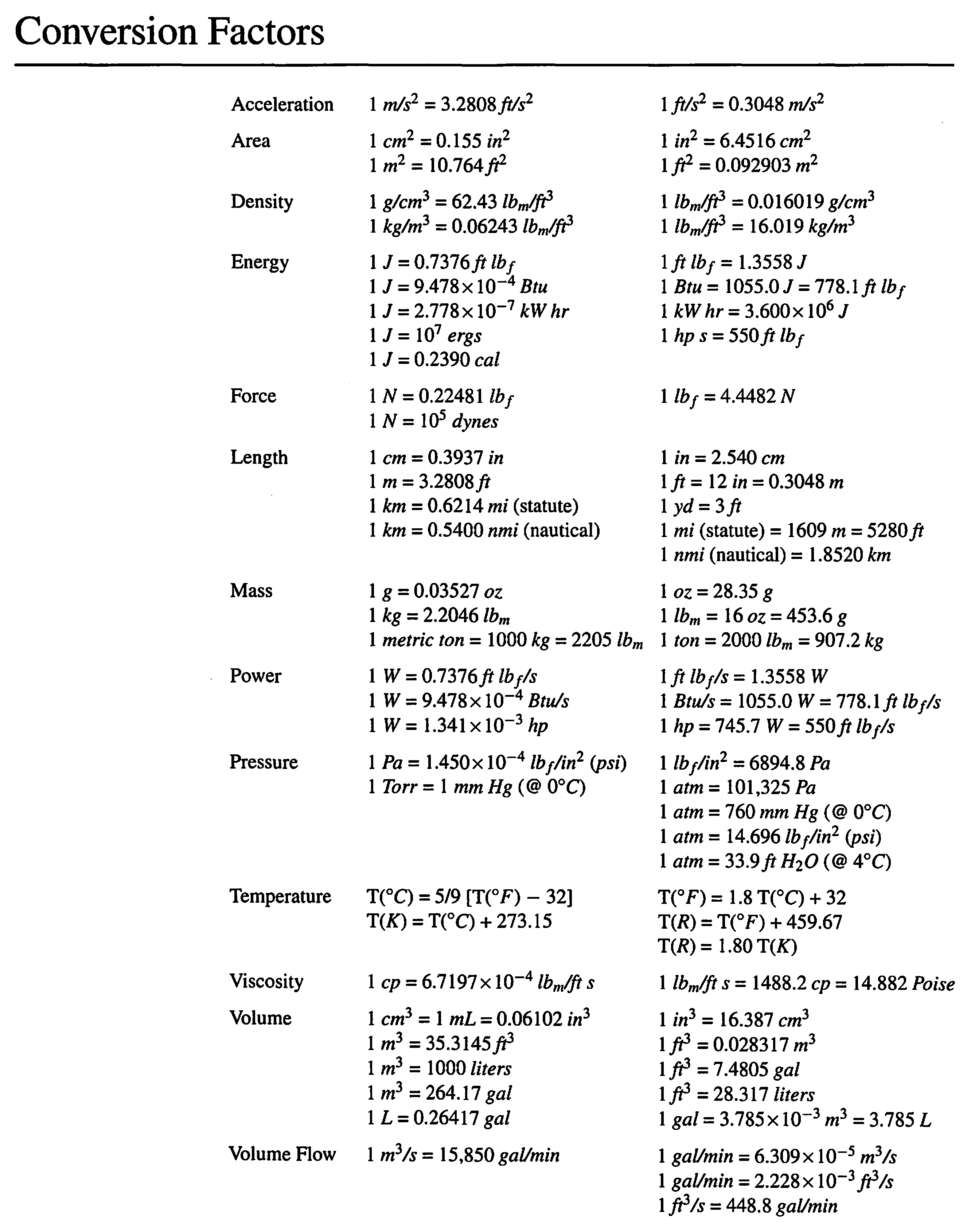
common conversion factors

Perry’s Chemical Engineers’ Handbook (highly recommended) and the CRC Handbook of Chemistry and Physics have many more conversion factors.

There are different, equivalent, ways that you will see units written.

For instance, the units for the heat transfer coefficient, \(h\), can be written numerous ways:

\(\mathrm{W \cdot m^{-2} \cdot K^{-1}}\)

\(\mathrm{W/m^{2}/K}\)

\(\si{W/m^{2}.K}\)

\(\mathrm{W/(m^{2} K)}\)

\(\mathrm{W/(m^{2} \cdot K)}\)

\(\mathrm{W m^{-2} K^{-1}}\)

\(\mathrm{W/m^{2} \cdot K}\)

\(\frac{\mathrm{W}}{\mathrm{m^{2} \cdot K}}\)

Example:

Convert \(\SI{5}{W/m^{2}.\degree C}\) to \(\si{Btu/s.ft^{2}.\degree F}\)

\[\SI{5}{\frac{\si{W}}{\si{m^{2}.\degree C}}} \cdot \left(\frac{\SI{3.412}{Btu/hr}}{\SI{1}{W}}\right) \left(\frac{\SI{1}{hr}}{\SI{3600}{s}}\right) \left(\frac{\SI{1}{m}}{\SI{3.28}{ft}}\right)^{2} \left(\frac{\SI{1}{\degree C}}{\SI{1.8}{\degree F}}\right) = \SI{2.447d-4}{\frac{\si{Btu}}{\si{s.ft^{2}.\degree F}}}\]

Exercise: Unit conversion

In their third most impressive prank to date, CBE students completely drained Horsetooth reservoir.

Horsetooth reservoir

As the water resource engineer in charge, it is your responsibility to refill it. ☹

A couple of eager interns working for you volunteer to go to the store to pick up the required water in 1-liter bottles.

  1. How many bottles should the interns bring back to completely refill the reservoir?

    Horsetooth reservoir has a capacity of 156,735 acre-feet of water.

    An acre-foot is a unit of volume commonly used in reference to large-scale water resources, such as reservoirs, lakes, and aqueducts.

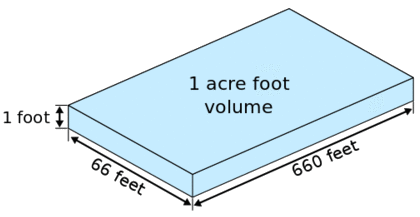
    acre foot

    Assume that there are \(\SI{43560}{ft^{2}}\) in \(\SI{1}{acre}\), \(\SI{12}{inches}\) in \(\SI{1}{ft}\), \(\SI{2.54}{cm}\) in \(\SI{1}{inch}\), \(\SI{100}{cm}\) in \(\SI{1}{meter}\), and \(\SI{1000}{liters}\) per \(\SI{1}{m^{3}}\).

    Write out the conversion equation in a clear, linear form.

  2. A 1-liter bottle of water is about \(\SI{11}{inches}\) tall.

    If the required bottles were placed end to end, how long would the stack be?

    In approximate terms, would the length be the distance from…

    1. sea level to the peak of Mount Everest (\(\approx \SI{8.9d3}{meters}\))?

    2. Fort Collins to Denver (\(\approx \SI{100}{km}\))?

    3. the Earth to the Moon (\(\approx \SI{380d3}{km}\))?

    4. the Earth to Mars (\(\approx \SI{55d6}{km}\) at their closest)?

    5. the Sun to Pluto (\(\approx \SI{4.4d9}{km}\) at their closest)?

Exercise: Unit conversion for custom units

In physics, the first radiation constant, \(c_{1}\), is approximately \(\SI{3.741d-16}{W.m^{2}}\), where \(\si{W}\) is watts ( \(\si{Joules/s}\) ), a unit of power.

Being a clever engineering student, you have developed a new system of units that you find more intuitive. The relevant units and conversion factors in your system are as follows:

Category

Unit

Conversion

power

workin_pretty_fast (wpf)

\(\SI{1}{wpf} = \SI{300}{W}\)

length

pretty_darned_small (pds)

\(\SI{1}{pds} = \SI{1.d-5}{m}\)

Express \(c_{1}\) in your system of units.

Solution