Reactor Design and Analysis¶

Perfection is achieved, not when there is nothing more to add, but when there is nothing left to take away.

—Antoine de Saint-Exupéry

Types of chemical reactors¶

Biological reactors¶

Cells as reactors

The human body as a reactor or reactor(s)

Traditional types¶

Batch reactor¶

In general, this type of reactor is charged via ports in the top of the tank.

While the reaction is carried out, nothing else is put in or taken out until the reaction is finished.

The tank may be heated or cooled by a jacket.

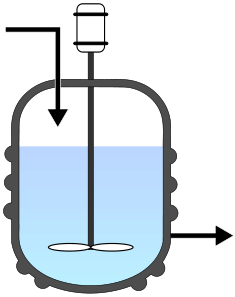
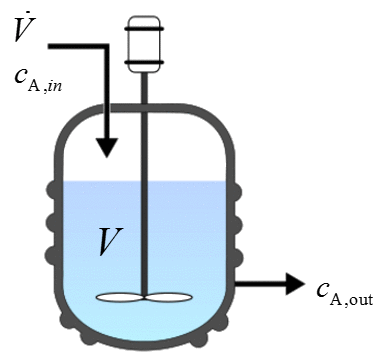
Continuously stirred tank reactor (CSTR)¶

This reactor type is generally run at steady state with continuous flow of reactants and products.

A common assumption is that there is uniform composition throughout the reactor.

Therefore, it is assumed that the exit stream has the same composition as that in the tank.

Plug-flow reactor¶

This reactor type is usually arranged as one long reactor or many short reactors in a tube bank.

It is generally assumed that there is little or no radial variation in reaction rate and concentration.

However, the concentration changes with length down the reactor.

In this course, we will focus our attention on CSTRs.

CSTRs are extremely common, with some of the reaction systems being

homogeneous liquid-phase reactions
heterogeneous gas-liquid reactions
heterogeneous liquid-liquid reactions
heterogeneous solid-liquid reactions
heterogeneous gas-solid-liquid reactions

Analysis and design¶

Typical problems:

Determine a reactor volume to achieve a certain product composition.
Given a reactor volume, predict the composition of the products leaving the reactor.

Quantifying reactor performance¶

There are several useful measures related to reactor and process performance: conversion, yield, and selectivity.

conversion, \(X\):

The fraction of a species that reacts. Conversion can be defined mathematically as

\[X = \frac{(\dot n_{\text{A, in}} - \dot n_{\text{A, out}})}{\dot n_{\text{A, in}}}\]

This is essentially

           the number of moles of A per time reacted
X =  ------------------------------------------------------
     the number of moles of A per time entering the reactor

yield, \(Y\):: Generally refers to the amount of a specific product formed per mole of reactant consumed
overall selectivity, \(S\):: Generally defined as the number of moles of desired product per the number of moles of undesired product

Care must be taken when computing yield and selectivity as there are a number of different definitions in common use.

Exercise:

In a reactor, if the conversion of species \(A\), \(X_{A}\), is \(0.75\), what is the ratio of inlet to outlet molar flow rate, \(\left (\frac{\dot n_{\text{A, in}}}{\dot n_{\text{A, out}}} \right )\)?

Under what condition would this ratio be the same as the ratio of inlet to outlet concentration, \(\left (\frac{c_{\text{A, in}}}{c_{\text{A, out}}} \right )\)?

Governing equations¶

As before, we have our general mass or mole balance:

Rate that       Rate that        Rate that     Rate that         Rate that
A enters    +   A is formed   =  A leaves   +  A is consumed  +  A accumulates
the system      in the system    the system    in the system     in the system

At steady state, there is no accumulation and we have the following:

Rate that       Rate that        Rate that     Rate that
A enters    +   A is formed   =  A leaves   +  A is consumed
the system      in the system    the system    in the system

These relationships will, of course, apply to all reactor types.

CSTRs¶

For a CSTR at steady state, we have

\[\begin{split}\sum_{\substack{\text{input}\\\text{streams}}} \dot n_{\text{A, in}} + r_{\text{formation, A}} = \sum_{\substack{\text{output}\\\text{streams}}} \dot n_{\text{A, out}} + r_{\text{consumption, A}}\end{split}\]

\[\begin{split}\sum_{\substack{\text{input}\\\text{streams}}} (\dot V \, c_{\text{A}})_{\text{in}} + r_{\text{formation, A}} = \sum_{\substack{\text{output}\\\text{streams}}} (\dot V \, c_{\text{A}})_{\text{out}} + r_{\text{consumption, A}}\end{split}\]

Relationship between rate of consumption and rate of reaction

\[r_{\text{consumption, A}} = r_{\text{reaction, A}} \, V\]

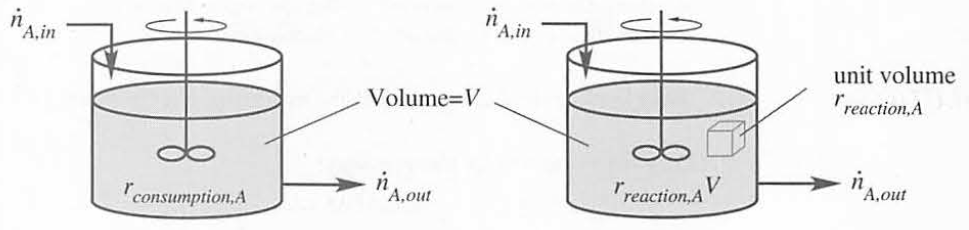
General steady-state CSTR design and analysis equations

\[V = \frac{r_{\text{consumption, A}}}{r_{\text{reaction, A}}}\]

Common special cases:

For a single input and output stream,

\[\dot n_{\text{A, in}} + r_{\text{formation, A}} = \dot n_{\text{A, out}} + r_{\text{consumption, A}}\]

and with no formation

\[\dot n_{\text{A, in}} = \dot n_{\text{A, out}} + r_{\text{consumption, A}}\]

and with constant density, \(\dot V_{\text{in}} = \dot V_{\text{out}} = \dot V\),

\[\dot V \, (c_{\text{A, in}} - c_{\text{A, out}}) = r_{\text{consumption, A}}\]

We also know that

\[r_{\text{consumption,A}} = r_{\text{reaction, A}} \, V\]

Combining the above leads to

Common special case CSTR design and analysis equation

\[\dot V \, (c_{\text{A, in}} - c_{\text{A, out}}) = r_{\text{reaction, A}} \, V\]

\[V = \frac{\dot V \, (c_{\text{A, in}} - c_{\text{A, out}})}{r_{\text{reaction, A}} }\]

Exercise: Reactions in CSTRs

To analyze an a specific reactor, we need an expression for the reaction rate, e.g.,

\[r_{\text{reaction, A}} = k_{r} \, f(c_{A}, \ldots)\]

In a CSTR, what concentration should we use in this equation? \(c_{\text{A,in}}\)? \(c_{\text{A,out}}\)? \(\bar c_{\text{A}}\)?

Why?

Residence time¶

Another very useful concept related to reactors is residence time, which is essentially the average time that a parcel of fluid spends in the reactor.

We can define the mean (average) residence time, \(\tau\), as

\[\tau = \frac{V}{\dot V}\]

Utilizing this definition, our special case CSTR analysis equation becomes

\[c_{\text{A,in}} - c_{\text{A,out}} = r_{\text{reaction,A}} \, \tau\]

Liquid mixing

We have assumed perfect mixing in our CSTRs.

As somewhat of an aside, let’s take a look at the mixing of high viscosity liquids in a Couette viscometer, a device that is useful in measuring the viscosity of fluids.

Exercise: CSTR analysis

Recall that our general reactor analysis equations are

\[V = \frac{r_{\text{consumption, A}}}{r_{\text{reaction, A}}}\]

Suppose that you have a reactor that carries out the reaction \(\ce{A + B -> C}\).

\(A\) is provided in excess such that the conversion is \(X_{A}\).

The reaction rate equation is

\[r_{\text{reaction, A}} = k_{r} \, c_{A}^{0.5}\]

The reactor has two inlets and one outlet. Inlet 1 contains \(A\) and a small amount of \(B\) and Inlet 2 contains pure \(B\).

For the stream associated with Inlet 1, you are given \(x_{A}\) and \(\dot V\).

For the stream associated with Inlet 2, you are given \(\dot V\).

The densities of each stream and molecular weights of all species are also known.

Assuming that the density of the system is not constant, what are the relevant analysis and design equations?

Exercise: CSTR design I - Given inlet and outlet conditions

Consider a CSTR that has one input and one output stream and where the fluid density is constant throughout the system.

The reactor is fed reactants \(E\) and \(F\) at a rate of \(\dot V = \SI{432}{L/min}\) and these reactants are converted to product \(J\).

The reaction rate equation is \(r_{\text{reaction, E}} = k_{r} \, c_{E} \, c_{F}^{2}\), where the estimated rate constant was determined to be \(k_{r} = \SI{6.1}{L^{2}.gmol^{-2}.s^{-1}}\).

The entering and leaving species concentrations are as follows:

\[\begin{split}\begin{align*} c_{E,in} &= \SI{0.95}{gmol/L} & c_{E,out} &= \SI{0.14}{gmol/L} \\ c_{F,in} &= \SI{2}{gmol/L} & c_{F,out} &= \SI{0.38}{gmol/L} \end{align*}\end{split}\]

Under these conditions,

What is the fractional conversion of \(E\), \(X_{E}\)?
What reactor volume, \(V\), is required?
What is the mean residence time under these operating conditions?
Challenge: Assume now that the mean residence time were cut in half. If \(c_{E, in}\), \(c_{F, in}\), \(c_{F, out}\), and the reactor volume, \(V\), remained the same as above. What would be the new fractional conversion of \(E\)?

Solution

Exercise: CSTR design II - Given stoichiometry

Consider a CSTR that has one input and one output stream and where the fluid density is constant throughout the system.

The reactor is fed reactants \(E\) and \(F\) at a rate of \(\dot V = \SI{432}{L/min}\) and these reactants are converted to product \(J\) according to the following reaction:

\[\ce{E + 2F -> J}\]