Process Variables

Furious activity is no substitute for understanding.

—H.H. Williams

Terminology

Inconsistent notation

One important ‘gotcha’ to keep in mind as you go through your CBE and other technical courses is that the notation is not consistent.

For instance, one book may use the symbol \(\theta\) to represent an angle, while another many use it to represent temperature. A book referring to density may use the symbol \(\rho\), while another may use the Latin letter D.

So, you will need to adapt your notation depending on the context. ☺

Here is a list of a few of the symbols and definitions we will use in this course.

Symbol

Definition

Units

\(m\)

mass

mass

\(m_{A}\)

mass of species \(A\)

mass

\(n\)

moles

moles

\(n_{A}\)

moles of species \(A\)

moles

\(V\)

volume of a process ‘container’

volume

\(MW_{A}\)

molecular weight of species \(A\)

mass/mole

\(\dot m\)

mass flow rate

mass/time

\(\dot n\)

molar flow rate

moles/time

\(\dot V\)

volumetric flow rate

volume/time

\(x_{A}\)

mass fraction of species \(A\)

unitless (mass/mass)

\(y_{A}\)

mole fraction of species \(A\)

unitless (moles/moles)

\(c_{A}\)

concentration of species \(A\)

moles/volume

\(\rho\)

density

mass/volume

\(P\)

pressure

force/area

\(T\)

temperature

temperature

Note that overdots represent rates (quantity per unit time).

More specifically, for the rates, we have the following definitions:

mass flow rate, \(\dot m\)

the mass of a material that passes a reference plane within a unit time interval

molar flow rate, \(\dot n\)

the number of moles of a material that passes a reference plane within a unit time interval

volumetric flow rate, \(\dot V\)

the volume of a material that passes a reference plane within a unit time interval

Useful relationships between some of these variables (KNOW THESE)

These relationships will help convert ‘what you know’ (the givens in a problem) into ‘what you need’ to formulate the equations and solve for the quantities of interest.

\[ \begin{align}\begin{aligned}m = \rho \, V\\x_{A} = \frac {m_{A}}{m}\\y_{A} = \frac {n_{A}}{n}\\\dot m = \rho \, \dot V\\c_{A} = \frac {n_{A}}{V}\\\dot m_{A} = x_{A} \, \dot m = MW_{A} \, \dot n_{A} = MW_{A} \, y_{A} \, \dot n = MW_{A} \, c_{A} \, \dot V\\\dot n_{A} = \frac {\dot m_{A}}{MW_{A}} = \frac {x_{A} \, \dot m}{MW_{A}} = y_{A} \, \dot n = c_{A} \, \dot V\end{aligned}\end{align} \]

Exercise

For the last two equations in the above box, write down the units for each term on the right- and left-hand sides of the equations. Assure that the units are consistent.

Important relationships for mass and mole fractions (KNOW THESE)

It is important to recognize that because they are fractions, the sum of mass (and mole) fractions across the chemical species in a system must be \(1\) .

More formally, given \(N\) chemical species…

\[ \begin{align}\begin{aligned}\sum_{i=1}^{N} x_{i} = 1\\\sum_{i=1}^{N} y_{i} = 1\end{aligned}\end{align} \]

Exercise: Calculating process and stream variables

  1. Assuming you know the density of a fluid stream is 2.0 kg/l and the volumetric flowrate is 10 l/hr, write out the equation using the appropriate symbols to find the total mass flowrate and compute the value. Convert units as needed.

  2. You are given the mass fraction of a chemical species in a process stream (0.3) and the total mass flowrate of the stream (100 kg/hr). Write out the equation using the appropriate symbols to find the mass flowrate of the species and compute the value. Convert units as needed.

  3. You know the molar flowrate of a chemical species is 5 gmol/s and the volumetric flowrate is 10 l/s. Write out the equation using the appropriate symbols to find the concentration of the chemical species and compute the value. Convert units as needed.

  4. You are told that the concentration of a chemical species is 2 kgmol/l, the molecular weight of the species is 200 kg/kgmol, and the mass flowate of the species is 800 g/s. Write out the equation using the appropriate symbols to find the total volumetric flowrate of the stream and compute the value. Convert units as needed.

Converting between Mole Fraction and Mass Fraction

In general, it is useful to assume some amount of materials for the calculation. We call this the basis of calculation or just basis.

Mole fraction to mass fraction

digraph mole { splines = ortho; bgcolor=transparent; rankdir=LR; node [shape=box]; s1 [label="Assume a basis \n of 100 moles"]; s2 [label="From the known \n mole fractions, \n calculate the \n number of moles \n of each species"]; s3 [label="Using the molecular \n weights, convert the \n moles into mass \n for each species"]; s4 [label="Compute the desired \n mass fractions \n or percentages"]; s1 -> s2; s2 -> s3; s3 -> s4; }

Exercise

As part of a physiology study, you have measured the composition of exhaled gas from a human subject and found the following mole percentages:

  • \(\ce{O2}\) : \(\SI{18}{mole \, percent}\)

  • \(\ce{N2}\) : \(\SI{78}{mole\, percent}\)

  • \(\ce{CO2}\) : \(\SI{4}{mole \, percent}\)

What are the mass fractions of these components?

Solution

Mass fraction to mole fraction

digraph mole { splines = ortho; rankdir=LR; bgcolor=transparent; node [shape=box]; s1 [label="Assume a basis \n of 100 mass units"]; s2 [label="From the known \n mass fractions, \n calculate the \n mass of each species"]; s3 [label="Using the molecular \n weights, convert the \n mass into moles \n for each species"]; s4 [label="Compute the desired \n mole fractions \n or percentages"]; s1 -> s2; s2 -> s3; s3 -> s4; }

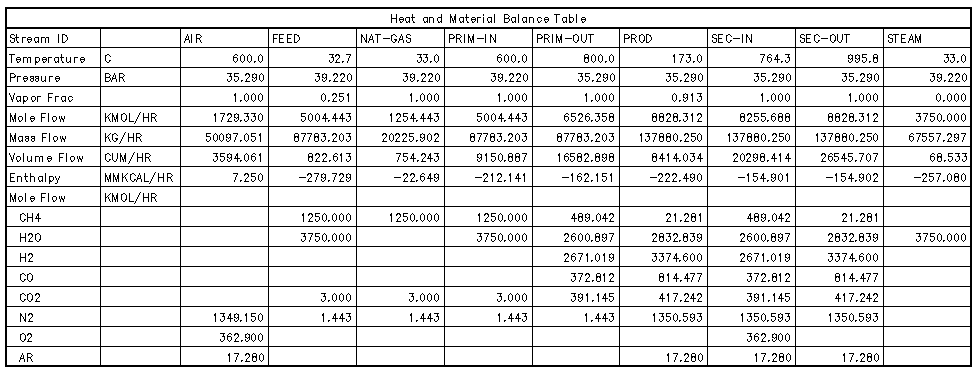
The stream table

The stream table lists important variables for all process streams in an organized, tabular format. The rows and columns are customized for the application. Typically, rows would be variables like composition, flow rate, temperature, and pressure; and columns would normally correspond to points before and after pieces of equipment.

A process stream table is also called a process flowsheet.

stream table