Reaction Kinetics¶

One man’s magic is another man’s engineering. Supernatural is a null word.

—Robert A Heinlein

Note

In general, experimental data are required to determine the rate equation for any given reaction

Reaction rates¶

What are some factors that influence chemical reaction rates?

Frequency of molecular collision
Orientation and force of the collision
Energy requirements of the reaction

Elementary reactions¶

An elementary reaction is characterized by a change from reactants to products that proceeds without identifiable intermediate species forming.

For an elementary reaction, the reaction rates for the forward and reverse paths are proportional to the concentration of species taking part in the reaction raised to the absolute value of their stoichiometric coefficients.

For example, if the following represents an elementary reaction,

\[\ce{A + B -> C + D}\]

then

\[\text{react}\text{ion rate} = r_{\text{rxn,A}} = k_{r} \, c_{A}^{n} \, c_{B}^{m}\]

This rate equation can then be used to predict the amount of \(A\) (or \(B\)) consumed or \(C\) (or \(D\)) formed per unit time, per unit volume (e.g., \(\frac{\text{moles of A}}{\text{time volume}}\)).

Gases

For gases, the equivalent of concentration is partial pressure, \(p\).

So, in this case, our rate equation would be written as

\[\text{react}\text{ion rate} = r_{\text{rxn,A}} = k_{r} \, p_{A}^{n} \, p_{B}^{m}\]

As a concrete example of a rate equation for an elementary reaction, consider

\[\ce{2NO + O2 -> 2NO2}\]

The resulting reaction rate expression is then \(r_{\text{rxn,NO}} = k_{r} \, c_{NO}^{2} \, c_{O_{2}}\)

Exercise: Reaction rate

Consider the above nitric oxide (\(NO\)) reaction.

Suppose that \(\SI{0.1}{moles}\) of \(\ce{NO}\) and \(\SI{0.5}{moles}\) of \(\ce{O2}\) were mixed in a \(\SI{1}{L}\) closed container.

Assuming that the value of the rate constant \(k_{r}\) is \(\SI{1.48d4}{L^{2}.mol^{-2}.sec^{-1}}\), what would be the reaction rate?

Solution

Stoichiometric reactions¶

For reactions that simply describe the observed overall stoichiometry, any correspondence between the stoichiometric coefficients and the reaction order is purely coincidental.

For instance, there could be multiple ‘hidden’ elementary reactions that lead to the observed stoichiometry.

Let’s look at a relevant example: the synthesis of methane (\(\ce{CH4}\)) from synthetic gas (\(\ce{CO}\) and \(\ce{H2}\)) over a ruthenium catalyst.

The overall reaction stoichiometry is

\[\ce{3H2(g) + CO(g) -> CH4 (g) + H2O (g)}\]

One postulated series of elementary reactions based on the surface chemistry, overall stoichiometry, and other observations is

\[\begin{split}\begin{align*} \ce{CO(g) + S &<=> CO_{ads}} \\ \ce{CO_{ads} + S &<=> C_{ads} + O_{ads}} \\ \ce{O_{ads} + H2(g) &-> H2O(g) + S} \\ \ce{H2(g) + 2S &<=> 2H_{ads}} \\ \ce{C_{ads} + H_{ads} &<=> CH_{ads} + S} \\ \ce{CH_{ads} + H_{ads} &<=> CH2_{,ads} + S} \\ \ce{CH2_{,ads} + H_{ads} &<=> CH3_{,ads} + S} \\ \ce{CH3_{,ads} + H_{ads} &-> CH4 (g) + 2S} \end{align*}\end{split}\]

Exercise:

With the above mechanism in mind, is it reasonable to assume that the reaction rate expression is \(r_{\text{reaction,CO}} = k_{r} \, c_{H_{2}}^{3} \, c_{CO}\)?

As an illustration of how the actual (measured) rate equation can differ from that which might be inferred from the overall stoichiometry reaction, consider

\[\ce{2CO + O2 -> 2CO2}\]

Through experimentation, the reaction rate expression was found to be \(r_{\text{reaction,CO}} = k_{r} \, c_{CO} \, c_{H_{2}O}^{0.5} \, c_{O_{2}}^{0.25}\), which reflects the fact that the actual reaction mechanism is quite complex, including the involvement of water in several intermediate steps.

Dependence of the rate constant on temperature¶

The temperature dependence of the reaction rate constant is often assumed to follow an Arrhenius form:

\[k_{r} = k_{0} \, e^{-E_{a}/(R\,T)}\]

where \(k_{0}\) is called the frequency factor (with the same units as \(k_{r}\)), \(E_{a}\) is the activation energy (in units of energy per mole), \(R\) is the universal gas constant, and \(T\) is the temperature at which the reaction takes place (expressed as absolute temperature).

Exercise:

Suppose that a chemical reaction occurs at \(\SI{100}{\degree C}\) and requires and activation energy, \(E_{A}\), of \(\SI{50}{kJ/mol}\).

What would the temperature have to be (in units of \(\si{\degree C}\)) to double the reaction rate?

The value of the universal gas constant, \(R\), is \(\SI{8.314d-3}{kJ/mol.K}\).

Reaction rates in biological systems¶

For enzyme-mediated reactions, the appropriate rate law is typically different from those listed above.

Here is a simplified representation of the interaction between the enzyme and substrate (the molecule that binds to the enzyme).

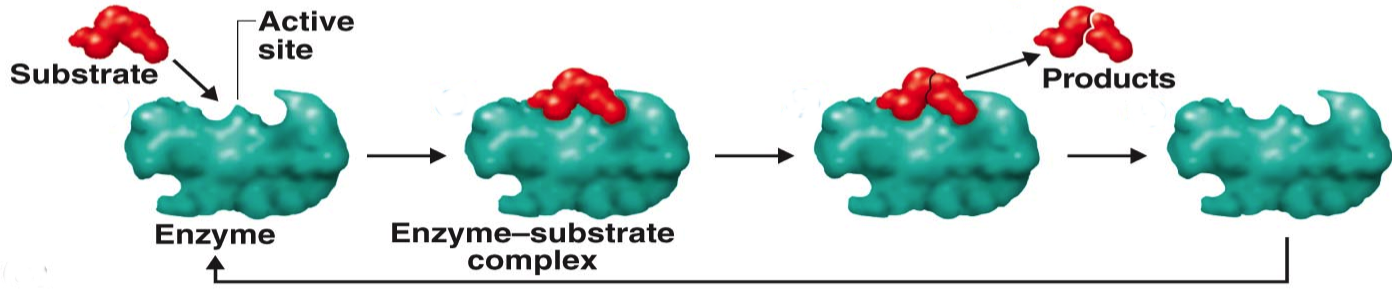
This overall interaction sequence is often represented schematically as

\[\ce{E + S <=> ES <=> E + P}\]

where \(E\) is the enzyme, \(S\) is the substrate , \(ES\) is the enzyme-substrate complex, and \(P\) is the product.

With this scheme in mind, the following expression (often called the Michaelis-Menten equation) can be derived:

\[v = \frac{dP}{dt} = \frac{V_{max} \, [S]}{K_{m} + [S]}\]

where \([S]\) is the concentration of the substrate, \(V_{max}\) is the maximum reaction velocity, and \(K_{m}\) is a constant that is derived from experimental measurements and represents the substrate concentration at \(v = (1/2) \, V_{max}\).

Exercise: Reaction rate for enzyme-mediated reactions

Consider the Michaelis-Menten equation above.

Make a plot of \(v\) (y-axis) versus \([S]\) (x-axis). What is the reaction order with respect to \(S\) at high and low values of \([S]\)?

How is this representative of the biochemistry?