Mass Transfer¶
Theories have four stages of acceptance: i) this is worthless nonsense; ii) this is an interesting, but perverse, point of view; iii) this is true, but quite unimportant; iv) I always said so.
—J.B.S. Haldane
Mass transfer: What is it?¶
Mass transfer
Mass transfer is mass in transit due to a species concentration gradient in a mixture.
By concentration gradient, we mean a spatial difference in the abundance of the chemical species.

Modes of mass transfer¶
diffusion
Diffusion is the macroscopic result of random molecular motion on a microscopic scale.
convection
Mass transfer by convection involves the transport of material between a boundary surface (such as solid or liquid surface) and a moving fluid or between two relatively immiscible, moving fluids.
Don’t confuse this phenomenon with the movement of mass caused by a chemical species simply being carried along in a fluid stream (advection).
Example: The story of engineering the contact lens
The cornea of the eye needs oxygen from the air
Mindful of mass transfer, here is the evolution of this important product.
‘Hard lenses’ (polymethylmethacrylate)
physically uncomfortable
inadequate oxygen diffusion (irritation, inflammation)
‘Soft lenses’ (hydrocarbon hydrogels)
physically more comfortable
inadequate oxygen diffusion
‘Oxygen permeable’ (siloxane)
physically uncomfortable
better oxygen diffusion
Latest generation (siloxane hydrogels)
physically more comfortable
better oxygen diffusion
Concentration profiles¶
A concentration profile is a sketch that indicates the magnitude of the concentration as a function of position.
This sketch is often superimposed on a process to indicate where these changes occur.
This is analogous to a velocity profile for fluid flow.
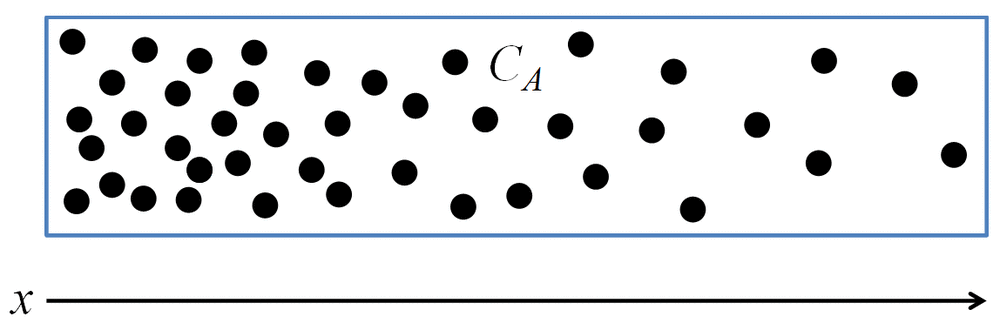
Exercise: Concentration profile
Based on the molecular distribution below, draw the concentration profile of species \(A\) as a function of \(x\):
Exercise: Quick (iClicker) questions
Mass transfer occurs because of gradient in what quantity?
temperature
pressure
fluid flow
concentration
The two main types of mass transfer are
diffusion and conduction
convection and diffusion
radiation and convection
conduction and radiation
A tank contains a uniform concentration of a chemical. The fluid in the tank is pumped into another tank. In CBE, is this movement of fluid and mass considered to be a form of mass transfer?
Yes
No
Demonstrations
Simulations of particle diffusion
Follow a given molecule and see how far it goes over time. For the multiple species case, try to follow a molecule in all three species and track how far each goes over time.
Very roughly speaking, squaring the distance traveled and dividing by the time over which you followed the molecule gives a fundamental measure commonly used to quantify mass transfer. Of course, we need to consider a very large number of molecules and do some appropriate averaging and scaling depending on the number of dimensions.
where \(D\) is the diffusion coefficient, \(r\) is the mean displacement of the particle, \(t\) is time, and \(d\) is the number of dimensions.
Diffusion¶
Describing diffusion quantitatively¶
Exercise: Diffusion
Suppose we have molecule \(A\) diffusing in a domain between boundary 1 and boundary 2, where \(c_{A,1}\) and \(c_{A,2}\) are held fixed.
What happens to \(c_{A}\) between boundary 1 and boundary 2 and what is the rate of diffusional mass transfer (\(\si{moles/time}\)) across some area \(A\)? Note that \(A\) represents an area \(y\) by \(z\) into the figure.

Here is a
particle simulation.
Fick’s law of diffusion
For a system in which there is pure diffusion only (no convection, no reactions, constant properties), the concentration profile is linear.
Thus, Fick’s law can be approximated by
Hence, the driving potential for diffusional mass transfer is \(c_{A,2} - c_{A,1}\).
In the above equations,
Variable |
Definition |
Typical units |
|---|---|---|
\(\dot N_{A,x}\) |
moles of species \(A\) transferred per unit time from location 1 to location 2 |
\(\si{mol/s}\) |
\(D_{AB}\) |
the ‘binary diffusivity’ (or diffusion coefficient) of species \(A\) through medium \(B\) |
\(\si{m^{2}/s}\) |
\(A\) |
the ‘face’ area through which transfer occurs |
\(\si{m^{2}}\) |
\(c_{A,2}-c_{A,1}\) |
the difference in concentration between locations 2 and 1 |
\(\si{mol/m^{3}}\) |
\(x_{2} - x_{1}\) |
the distance between locations 2 and 1 |
\(\si{m}\) |
As a reminder, the area for mass transfer is not the ‘edge-view’ area, but the ‘face-view’ area:
Adjustments to the area for mass transfer
When we consider the area for mass transfer, \(A\), we need to consider that some of the apparent area may not be available to transport mass.
For instance, imagine a porous membrane with a pore fraction of \(\epsilon_{\text{pore}}\). In this case, the actual area available for mass transfer is only the porous fraction of the total, and thus,
We will generally write \(A\) in our governing rate equations, but keep in mind this distinction and include surface area adjustments when necessary.
Exercise: Fick’s law
Why is there a minus sign in Fick’s law?
The diffusion coefficient¶
One of the big unknowns in Fick’s equation above is the diffusion coefficient, \(D_{AB}\).
The diffusion coefficient (or diffusivity) is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion).
On a theoretical basis, the diffusion coefficient is proportional to the mean squared displacement divided by the time elapsed: \(D \propto \frac{\left< x^{2} \right>}{t}\)
How do we determine it?
Experiments
Theory
Estimation
Properties will influence the diffusion coefficient of molecule \(A\) in solution \(B\):
molecular size of \(A\) and/or \(B\)
molecular weight of \(A\) and/or \(B\)
molecular properties (e.g., charge, ionic strength, dipole moment) of \(A\) and/or \(B\)
temperature
pressure
Exercise:
What systems can demonstrate diffusion?
gas/gas ?
gas/liquid ?
gas/solid ?
liquid/liquid ?
liquid/solid ?
solid/solid ?
What are some typical values of diffusion coefficients?
As a reminder, these values are measured in \(L^{2}/t\).
Which coefficients will be largest?
By how much? Take a guess.
Exercise: Diffusion in a cell membrane
Cell membranes play a significant role in determining the rate of chemical transport into and out of the cell. Major components of the cell membrane are phospholipids, amphipathic molecules which form bilayers (shown below) with a hydrophobic core surrounding the cell. The hydrophobic tails produce what is essentially a separate ‘organic’ phase surrounded by an aqueous environment inside and outside the cell. Small, uncharged molecules such as urea cross this membrane by simple diffusion.

Assume that urea is diffusing out of the cell at steady state and that the environment both inside and outside of the cell is well mixed.
Qualitatively sketch the concentration profile of urea in the cell, across the membrane and into the surrounding aqueous environment.
What information (parameters) would you need to estimate the rate of mass transfer of urea from the cell? Discuss how each parameter would influence the diffusion rate and why.
Using the information from part b, propose an equation for the rate of diffusion of urea from the cell at steady state.
Mass Convection¶
As we saw earlier, mass transfer refers to mass in transit due to a species concentration gradient in a mixture, and mass convection is one of the mechanisms for this transit.
Mass transfer by convection involves the transport of material between a boundary surface (such as solid or liquid surface) and a moving fluid or between two relatively immiscible, moving fluids.
Convective mass transfer is really diffusion (the random movement of molecules) in combination with advection (molecules being carried along with the motion of the fluid).
Boundary layers
To better understand mass transfer via convection, it is important to consider boundary layers in fluids flowing over surfaces.
Newton’s law of cooling¶
To quantify the rate of mass transfer owing to convection, we can make use of Newton’s law of cooling (which, as we will see, also applies to convective heat transfer).

Newton’s law of cooling for mass transfer
Hence, the driving potential for convective mass transfer is \(c_{A,s} - c_{A,\infty}\)
In the above equations,
Variable |
Definition |
Typical units |
|---|---|---|
\(\dot N_{A,x}\) |
moles of species \(A\) transferred per unit time from the surface to the bulk fluid far from the surface |
\(\si{mol/s}\) |
\(h_{m}\) |
the mass transfer coefficient |
\(\si{m/s}\) |
\(A\) |
the area (cross section) through which transfer occurs |
\(\si{m^{2}}\) |
\(c_{A,s}-c_{A,\infty}\) |
the difference in concentration between the surface and bulk fluid |
\(\si{mol/m^{3}}\) |
Questions:
In what ways is Newton’s law of cooling a major simplification.
What factors influence the mass transfer coefficient?
Exercise:
You are interested in experimentally determining the mass transfer coefficient for a particular application. You have a device where a number of system properties can be varied: the surface area for mass transfer, the molar rate of transfer, and the bulk concentration of the species of interest. The surface concentration is maintained at \(\SI{10.5}{mol/m^{3}}\). Given the following experimental values, what is a reasonable estimate of the mass transfer coefficient in units of \(\si{m/hr}\)?
Surface area (\(\si{cm^{2}}\)) |
Transfer rate (\(\si{mol/s}\)) |
Bulk concentration (\(\si{mol/m^{3}}\)) |
\(1000\) |
\(\num{1.00d-06}\) |
\(9.00\) |
\(1500\) |
\(\num{1.80d-06}\) |
\(8.68\) |
\(2000\) |
\(\num{1.30d-06}\) |
\(9.52\) |
\(2500\) |
\(\num{1.10d-06}\) |
\(9.84\) |
Concentration profiles for convective mass transfer¶
Exercise: Concentration profiles for convective mass transfer
Concentration profiles for convective mass transfer When considering convective mass transfer, it is critical to keep in mind the boundary layer. This concentration boundary layer is very similar to the hydrodynamic boundary later.
What is happening in the boundary layer? What is happening outside of the boundary layer?
With this in mind, sketch out the concentration profile, starting from near the surface to well out in the surrounding bulk fluid.
Of course, the shape of the profile depends on many factors: fluid velocity, fluid properties, surface shape, …
Combined diffusion and convection¶
What do we do in cases like this hypothetical mass transfer device?
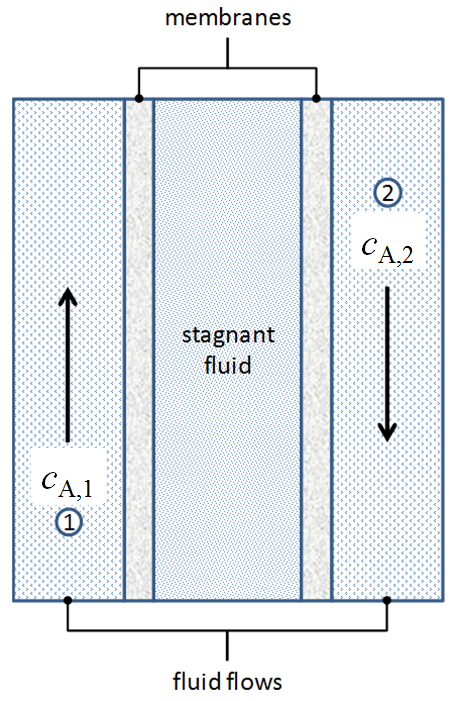
Given the concentrations of species A at points 1 and 2 (\(c_{A1}\), \(c_{A2}\)), how do we compute the rate of mass transfer between them? We need to consider convective and diffusive mass transfer in multiple media.
Concentration profiles¶
The concentration profile owing purely to diffusion through a medium with constant material properties and no reaction is linear.
The concentration profile owing to convective mass transport shows a sharp change right near the surface as described for boundary layers.
Profiles with combined mechanisms usually have to match at interfaces (same concentration and slope).
Exercise: Concentrations for combined mechanisms
Sketch out the concentration profile through the device pictured above when \(c_{A,1}\) is greater than \(c_{A,2}\) and the fluid in stream 1 and stream 2 are relatively well mixed.
Matching mass transfer rates
At steady state, the amount of mass per time passing through each ‘plane’ must be equal, otherwise the system would have accumulation.
If the mass transfer area, \(A\), is equal for all of these planes (as for the geometry above), the mass per time per area (or mass flux) must be equal. Is this true for a cylindrical geometry?
Resistances¶
We can use concepts of mass transfer resistance to make the analysis of mass transfer with combined mechanisms much easier.
Definition of resistance
A resistance is the driving potential (or driving force) divided by the transfer rate:
We are probably familiar with Ohm’s law, in which the driving potential is the voltage and the transfer rate is the current, leading to
For mass transfer, our driving potential is an appropriate concentration difference, \(\Delta c\), and the transfer rate is the molar transfer rate, \(\dot N_{A}\).
Exercise:
For both diffusion and mass convection,
what is the driving potential (concentration difference)?
what is the molar transfer rate equation?
what is the resulting expression for the mass transfer resistance?
Like in electrical circuits, resistances can be added directly if they are in series:
For the above mass transfer device, there are five resistances between our concentration measurements (\(c_{A,1}\), \(c_{A,2}\))
The resistances \(R_{\text{flowing fluid 1}}\) and \(R_{\text{flowing fluid 2}}\) are for convective processes, while those for \(R_{\text{membrane 1}}\), \(R_{\text{stagnant fluid}}\), and \(R_{\text{membrane 2}}\) are for diffusive processes.
So, to compute the rate of mass (molar) transfer, we can use the following:
Resistance equations
where, for resistances in series, we have
and
Note
The equations we have developed are applicable only to systems being analyzed in rectangular Cartesian coordinate systems. When we analyze heat transfer resistances, we will examine changes that are needed for other coordinate systems (e.g., cylindrical coordinates)
Exercise: Mass transfer resistances
You have been assigned to improve the efficiency of a chemical separations device. The team that improves the efficiency most will win an all-expense-paid trip to the destination of their choice. A schematic of the device is as follows:

Baseline characteristics
\(D_{\text{A/hydrogel}} = \SI{5d-4}{cm^{2}/s}\) |
\(D_{\text{A/membrane}} = \SI{7d-5}{cm^{2}/s}\) |
\(L1 = \SI{5}{mm}\) |
\(L2 = \SI{1}{mm}\) |
\(h_{m} = \SI{0.002}{cm/s}\) |
\(A = \SI{1}{m^{2}}\) |
Your team has developed technologies leading to three design options:
improved hydrogel diffusivity: 4 time the baseline value
improved membrane diffusivity: 3 times the baseline value
increased mass transfer coefficient: 6 times the baseline value
Assuming that \(c_{A,1} > c_{A,2}\), make a sketch of the expected concentration of \(A\) in the device.
Which single option will you choose to achieve the best improvement of device performance?
One useful measure of performance is the mass transfer rate (moles/min).
