Heat Transfer

In the beginning the Universe was created. This has made a lot of people very angry and been widely regarded as a bad move.

—Douglas Adams

Heat transfer

Heat transfer is thermal energy in transit due to a temperature difference.

A topic you may have touched on in Chemistry is thermodynamics. Thermodynamics deals with equilibrium processes and endpoints. It doesn’t give us rates. Heat transfer deals with temperature gradients and non-equilibrium phenomena.

Note

Remember to use Kelvins (or Rankine) for heat transfer calculations. This is especially important in looking at radiative heat transfer.

Modes of heat transfer (a.k.a. heat transport)

  • conduction

  • convection

  • radiation

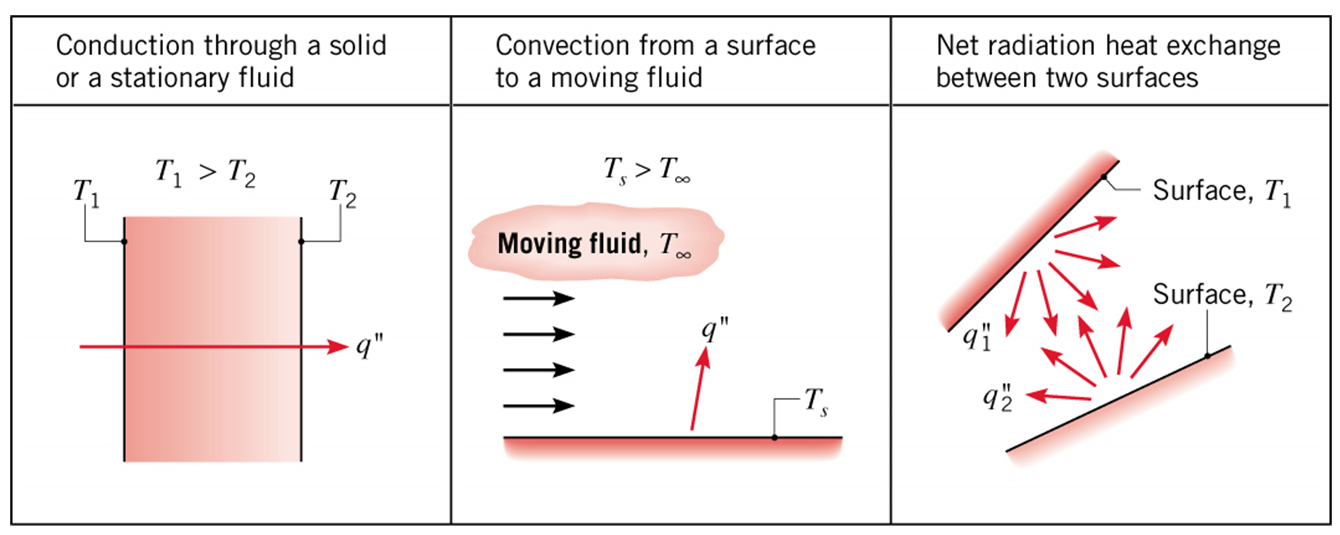
heat transfer modes

Conduction: Heat transfer in a solid or a stationary fluid (gas or liquid) due to the random motion of its constituent atoms, molecules and /or electrons.

Convection: Heat transfer due to the combined influence of bulk (advection) and random motion for fluid flow over a surface.

Radiation: Energy that is emitted by matter due to changes in the electron configurations of its atoms or molecules and is transported as electromagnetic waves (or photons).

Notes and terminology

Conduction and convection require the presence of temperature variations in a material medium.

Although radiation originates from matter, its transport does not require a material medium and occurs most efficiently in a vacuum.

The heat rate, \(\dot Q\), is the amount of heat moving through a surface or plane per unit time. Typical units would be \(\si{J/s}\).

The heat flux, \(\dot Q/A\), is the amount of heat moving through a surface or plane per unit time per unit area. Typical units would be \(\si{J/s\cdot m^{2}}\).

Conduction

Conduction is the heat transfer analogue of diffusion in mass transfer.

It is the heat transfer in a solid or a stationary fluid (gas or liquid) due to the random motion of its constituent atoms, molecules and /or electrons.

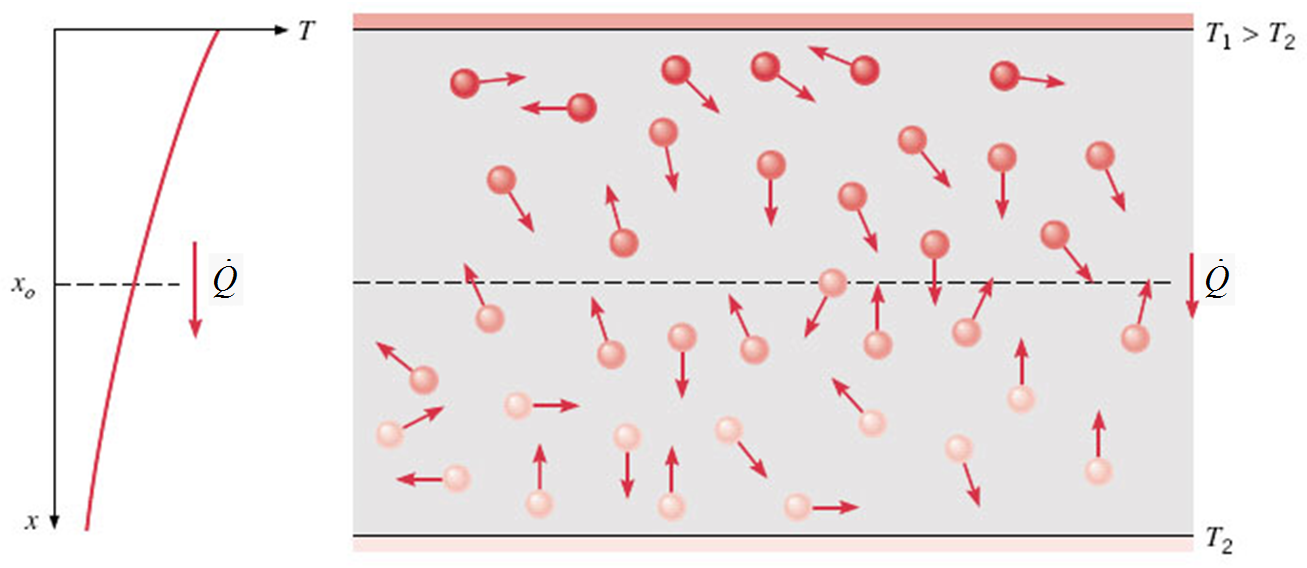
heat transfer conduction

Exercise: Thought experiment (Gedankenexperiment)

heat transfer conduction apparatus

  • heat a material at \(x=0\)

  • insulate on the edges

  • vary the input power

  • measure the temperature at \(x = 0\) and \(x = L\)

Sketch a plot of the heat flux (\(\dot Q / A\)) versus \((T_{1}-T{2}) / L\)

What can we infer from these data?

Describing conduction heat transfer quantitatively

Joseph Fourier: a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations.

Fourier’s law

\[\begin{split}\begin{align*} \dot Q_{\text{cond}} &= -k \, A \, \frac{dT}{dx} \\ &\approx -k \, A \, \frac{T_{2}-T_{1}}{x_{2}-x_{1}} = -k \, A \, \frac{\Delta T}{\Delta x} \end{align*}\end{split}\]

where

\(\dot Q_{\text{cond}}\)

=

conduction heat-transfer rate through area A in the x direction between locations 1 and 2

\(\si{J/s}\) (or \(\si{W}\))

\(A\)

=

cross-sectional area through which conduction occurs

\(\si{m^{2}}\)

\(k\)

=

the thermal conductivity of the material

\(\si{W/m.K}\)

\(T\)

=

temperature

\(\si{K}\)

Note that Fourier’s law is the heat transfer analogue to Fick’s law for diffusion mass transfer.

Thermal conductivity

Like the diffusion coefficient, \(D_{AB}\), for mass transfer, the thermal conductivity, \(k\), is a material-dependent, constant of proportionality in Fourier’s law.

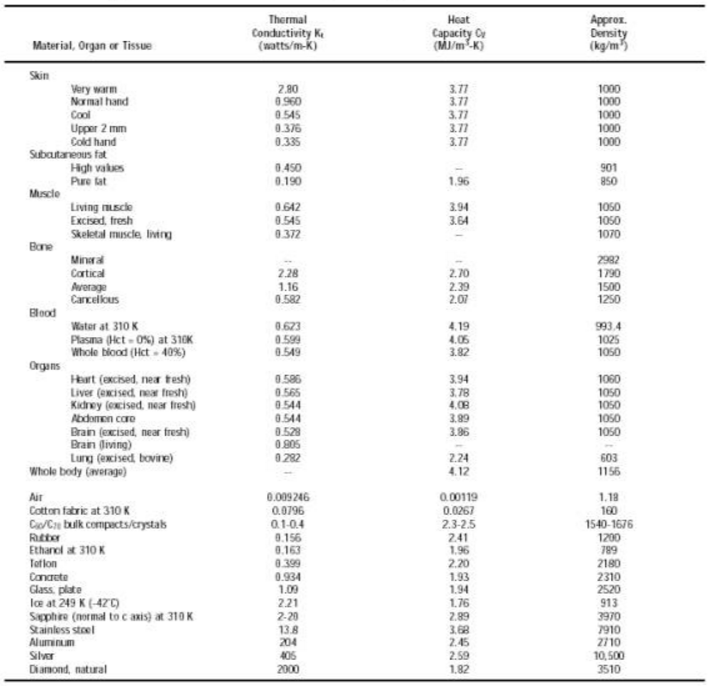
Here are some values of the thermal conductivity for various materials:

thermal conductivity values

Thermal conductivity values have even been measured for various biological tissues:

thermal conductivity values for tissues

Quiz

  1. Fourier’s law for heat transfer is analogous to what equation for mass transfer?

    1. Fick’s law of diffusion

    2. the ideal gas law

    3. Newton’s law of cooling

    4. the Stefan-Boltzman equation

  2. The proportionality constant in Fourier’s law is the

    1. dispersion factor

    2. diffusion coefficient

    3. thermal conductivity

    4. heat capacity

  3. Metals like copper have a thermal conductivity at room temperature that is closest to which of the following:

    1. \(\SI{0.05}{W/m.K}\)

    2. \(\SI{5}{W/m.K}\)

    3. \(\SI{500}{W/m.K}\)

    4. \(\SI{5d4}{W/m.K}\)

Exercise: Thermal conductivity

You have just been selected as a junior engineer at Marvel Labs, Inc. Your first job is to characterize the thermal properties of a new metal alloy to replace Adamantium (a key component in the bodies, armor, and weapons of a number of notable superheros). A schematic of your apparatus is

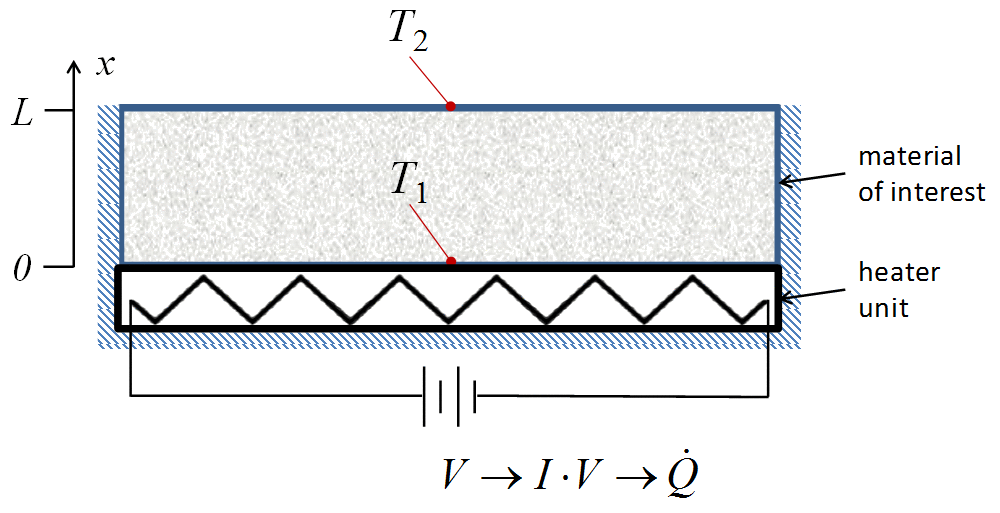
heat transfer conduction apparatus

You can vary the power to the heater and the cross-sectional area and thickness of the material in your tests.

Based on the following data, what is the approximate value of the thermal conductivity of the new material (\(\si{W/m..K}\))?

\(\dot Q\ (mW)\)

\(A\ (cm^{2})\)

\(L\ (mm)\)

\(T_{1}\ (K)\)

\(T_{2}\ (K)\)

150

4

2

353

323

162

4

2

363

333

142

9

4

343

313

155

9

4

403

373

232

16

6

503

473

Solution

Convection

Convection is the heat transfer analogue of mass transfer convection.

Convective heat transfer is heat transfer due to the combined influence of bulk and random motion for fluid flow over a surface.

Consider flow across a flat surface. What do the velocity and temperature profiles look like?

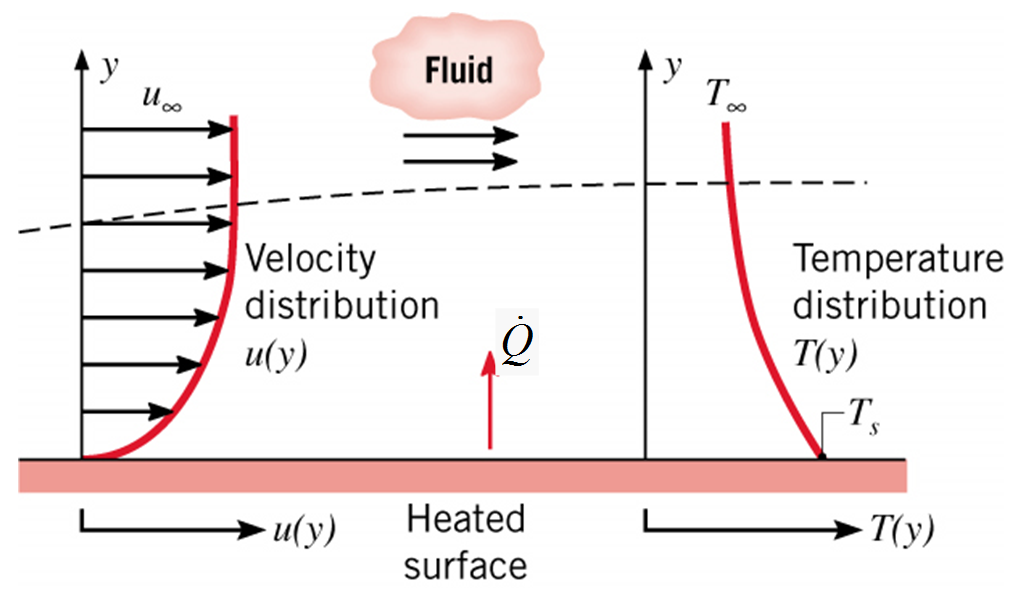
heat transfer convection profiles

Describing convective heat transfer quantitatively

Newton’s law of cooling

\[\dot Q_{\text{conv}} = h \, A\, (T_{s} - T_{\text{bulk fluid}}) = h \, A\, (T_{s} - T_{\infty})\]

where

\(\dot Q_{\text{conv}}\)

=

convection heat-transfer rate through area A in the x direction between locations 1 and 2

\(\si{J/s}\) (\(\si{W}\))

\(A\)

=

cross-sectional area through which conduction occurs

\(\si{m^{2}}\)

\(h\)

=

the heat transfer coefficient

\(\si{W/m^{2}.K}\)

\(T\)

=

temperature

K

The heat transfer coefficient

Like the mass transfer coefficient, the heat transfer coefficient in strongly influenced by the boundary layer. In particular, it depends on the geometry, flow conditions, fluid, and process.

You will see in future courses how these coefficients can be measured and predicted. They are not constant for a type of fluid; they depend on the flow conditions, geometry, and fluid properties.

Here are some typical values:

heat transfer coefficient values

Quiz

  1. Newton’s law of cooling describes heat transfer as proportional to what quantity?

    1. molecular weight

    2. pressure

    3. temperature difference

    4. volume

  2. The proportionality constant in Fourier’s law is the

    1. thermal conductivity

    2. diffusion coefficient

    3. heat transfer coefficient

    4. heat capacity

  3. Appropriate units for the heat transfer coefficient are

    1. \(\si{W/m^{2}.K}\)

    2. \(\si{W/m.K}\)

    3. \(\si{s/m^{3}}\)

    4. \(\si{J/kg.K}\)

Exercise: Temperature profiles for convective heat transfer

Examine the following diagram carefully

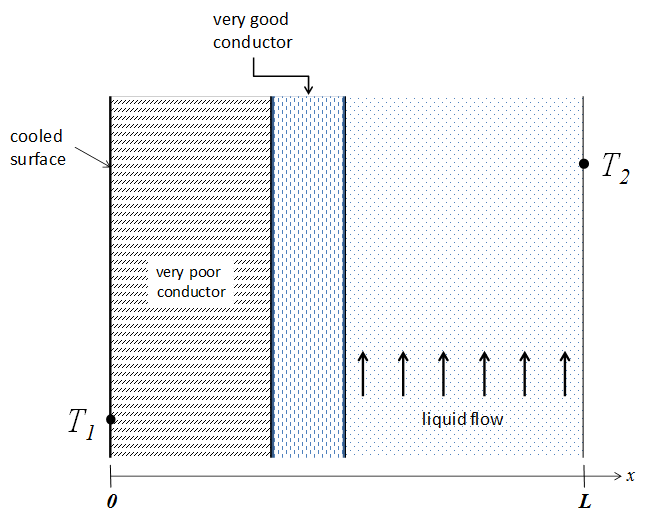
convective heat transfer profile

  1. Sketch out the temperature profile from \(x = 0\) to \(x = L\).

  2. Sketch out the profile in the case where the material properties, but not the dimensions, of the conductors were switched.

In both cases, justify the shapes you drew (values, slope, curvature).

Radiation

Radiation is energy that is emitted by matter due to changes in the electron configurations of its atoms or molecules and is transported as electromagnetic waves (or photons).

There is no mass transfer analogue to radiation.


The electromagnetic spectrum and the range of wavelengths involved in radiative heat transfer:

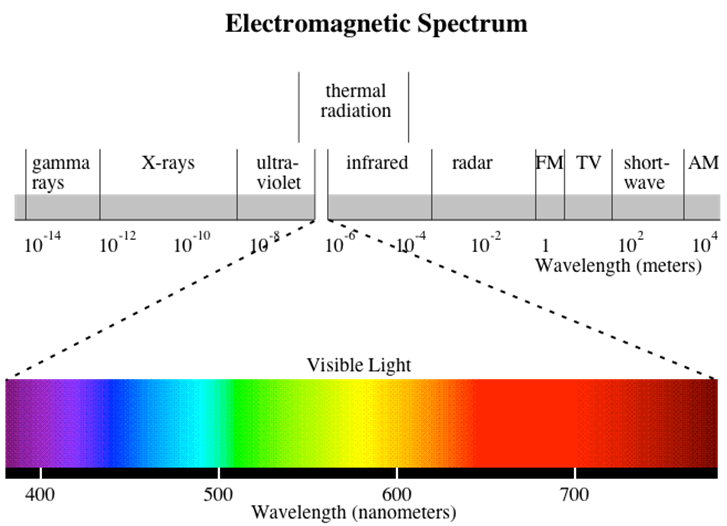
electromagnetic spectrum heat transfer radiation wavelengths

Relevant phenomena associated with photon interactions with surfaces are reflection, absorption, and transmission:

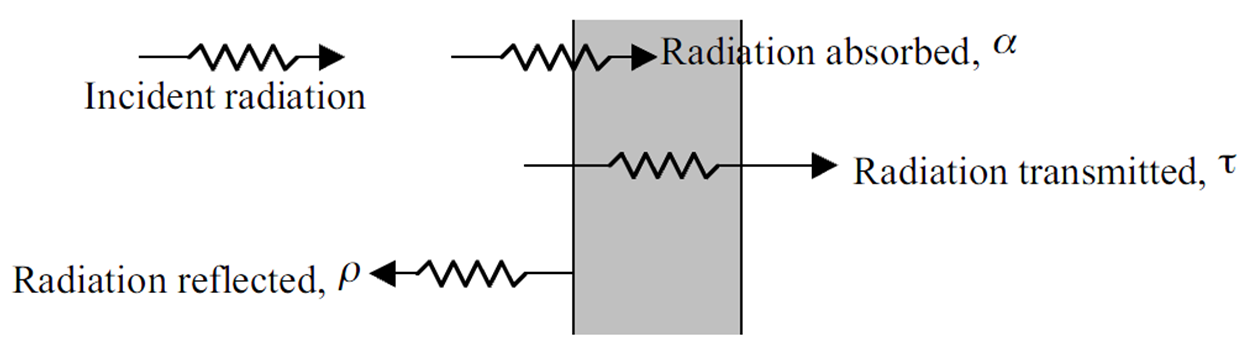
heat transfer radiation phenomena

Describing radiation heat transfer quantitatively

Radiation rate equation

The net radiation heat flux from the surface due to exchange with the surroundings is

\[\dot Q_{\text{rad}} = \epsilon \, \sigma \, A \, (T_{s}^{4} - T_{\text{sur}}^{4})\]

where

\(\dot Q_{\text{rad}}\)

=

convection heat-transfer rate through area A in the x direction between locations 1 and 2

\(\si{J/s} = \si{W}\)

\(A\)

=

cross-sectional area through which conduction occurs

\(\si{m^{2}}\)

\(\epsilon\)

=

the emmisivity of the surface

dimensionless

\(\sigma\)

=

the Stefan-Boltzmann constant

\(\SI{5.67d-8}{W/m^{2}.K^{4}}\)

\(T_{s}\)

=

temperature of the surface

\(\si{K}\)

\(T_{sur}\)

=

temperature of the surrounding surfaces

\(\si{K}\)

Important note: \(T_{\infty}\) and \(T_{sur}\) are not the same. \(T_{\infty}\) indicates a free stream (liquid/gas) temperature that drives convection, while \(T_{sur}\) is the temperature of the surrounding surface involved in radiation.

Combined mechanisms or modes

Heat transfer mechanisms (conduction, convection, radiation) can often occur simultaneously.

They can be occur in series and/or parallel.

As we saw for mass transfer, resistance concepts can be useful when analyzing combined mechanisms, especially when they occur in series.

Resistances

As a reminder,

Definition of resistance

The resistance is the driving potential (or driving force) divided by the transfer rate:

\[\text{resistance} = \frac{\text{driving potential}}{\text{transfer rate}}\]

Exercise: Heat transfer resistances

  • In the area of heat transfer, what is the transfer rate?

  • What are the specific expressions for the rate for conduction and convection heat transfer?

  • What is the driving force (also known as the driving potential) in each case?

  • What are the expressions for the resistances?

  • Finally, what are the units of heat transfer resistance?

Solution

Resistances: The effect of the coordinate system

Although the driving force may remain the same, the expression for the transfer rate may vary based on the coordinate systems.

Cartesian coordinate system

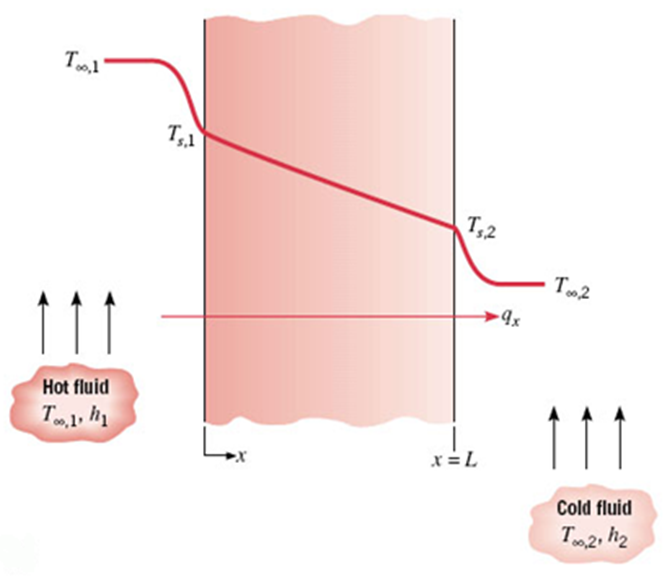
heat transfer resistances cartesian

The heat transfer rate is

\[Q_{\text{cond}} = \frac{k \, A}{L} \left( T_{S,1} - T_{S,2}\right)\]

Consequently, the heat transfer resistance due to conduction is

\[R_{\text{cond}} = \frac{L}{k \, A}\]

The total resistance for this case (convection + conduction + convection) is

\[R_{\text{tot}} = \frac{1}{h_{1} \, A} + \frac{L}{k \, A} + \frac{1}{h_{2} \, A}\]

Cylindrical coordinate system

In the following, note that \(L\) is the length of the cylinder, not the appropriate distance over which radial conduction occurs, which is \(r_{2} - r_{1}\).

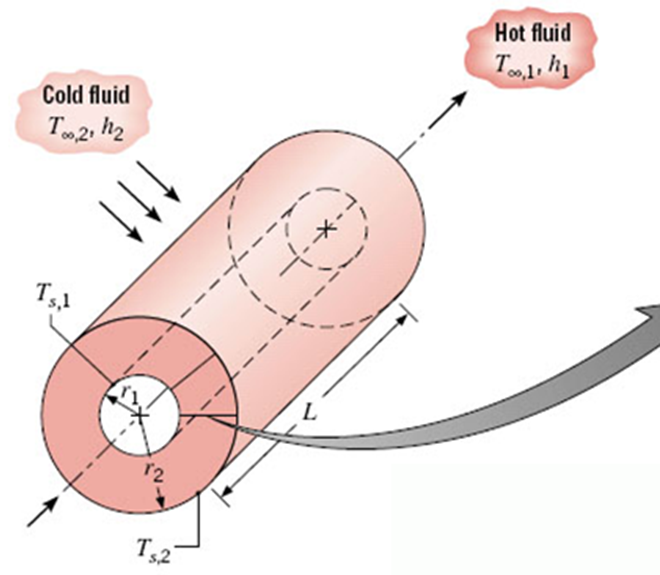
heat transfer resistances cylindrical

At steady state, the heat transfer rate across a cylinder of one radius must be equal to that for any other radius.

This leads to a temperature profile in \(r\) that is not linear, but has a shape like this:

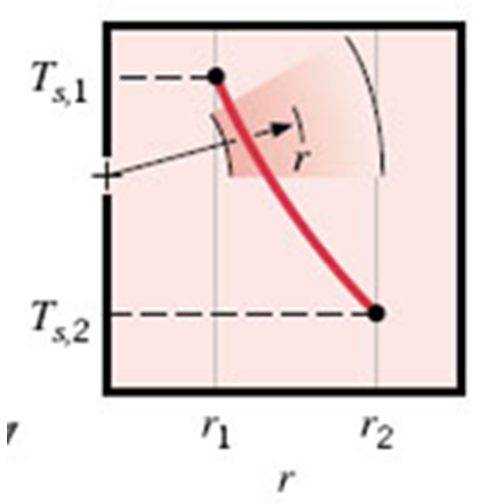
heat transfer cylindrical temp profile

The equation for the temperature profile is

\[T(r) = \frac{T_{s,1} - T_{s,2}} {\ln \left( r_{1}/r_{2} \right)} \ln \left( \frac{r}{r_{2}} \right) + T_{s,2}\]

The corresponding heat transfer rate is

\[\dot Q = \frac {2 \pi \, L \, k \left( T_{s,1} - T_{s,2}\right)} {\ln \left( r_{2}/r_{1} \right)}\]

and the heat transfer resistance is

\[R_{\text{cond}} = \frac{\ln \left( r_{2}/r_{1} \right)} {2 \pi \, L \, k}\]

The total resistance for this case (convection + conduction + convection) is

\[R_{\text{tot}} = \frac{1}{h_{1} \, A_{1}} + \frac{\ln \left( r_{2}/r_{1} \right)} {2 \pi \, L \, k} + \frac{1}{h_{2} \, A_{2}}\]

Note that the relevant heat transfer areas are different for each term.

Exercise: Questions

  1. If \(T_{s}\) is the temperature of the surface, \(T_{\infty}\) is the temperature of the fluid over the radiating surface, and \(T_{\text{sur}}\) is the temperature of the surrounding surfaces, what is the driving force for radiation heat transfer?

  1. \(\left(T_{s}^{4} - T_{\text{sur}}^{4} \right)\)

  1. \(\left(T_{s}^{4} - T_{\infty}^{4} \right)\)

  1. \(\left(T_{s} - T_{\infty} \right)\)

  1. \(\left(T_{s} - T_{\text{sur}} \right)\)

  1. The thermal resistance for heat conduction, \(R_{\text{cond}}\), in a tube wall is given by

  1. \(\frac{r_{2}-r_{1}}{L \ k}\)

  1. \(\frac{L}{k \ A}\)

  1. \(\frac{\ln \left( r_{2}/r_{1} \right)}{2 \pi \ L \ k}\)

  1. \(\frac{1}{h \ A}\)

  1. What is the value of y after the following MATLAB code has been executed?

    x1 = [1,2,3;4,5,6;7,8,9]
x2 = x1.^2
y = x2(2,3)

  1. [2 3]

  1. 36

  1. [4 9]

  1. 64

Exercise: Heat loss from a person

Consider a person standing in a breezy room. Determine the total rate of heat transfer from this person if the exposed surface area and temperature are \(\SI{1.6}{m^{2}}\) and \(\SI{29}{\degree C}\), respectively.

Assume that the convection heat transfer coefficient is \(\SI{6}{W/m^{2}.K}\) and the emissivity of a person of \(0.95\).

The air temperature in the room is maintained at \(\SI{22}{\degree C}\) at all times of the year.

In summer, the wall and ceiling temperatures are observed to be \(\SI{25}{\degree C}\), while in winter, they are \(\SI{10}{\degree C}\).

Explain why we might feel chilled in the winter even when the thermostat and interior temperature are the same as in the summer.

Assume:

  • steady state

  • the person is completely surrounded by interior surface of room

  • heat conduction to the floor from the feet is negligible

Sketch out this scenario, including heat flows and temperatures.

Do the heat transfer mechanisms occur in parallel or series?

Do we need resistance concepts to analyze this?

Solution