FLUCTUATIONS IN NANOSCALE SYSTEMS
SPECTRAL CONTENT OF NON-STATIONARY RANDOM WALKS
We have analyzed the spectral content of different random walks. The power spectral densities of Brownian motion and fractional Brownian motion were evaluated at the level of individual trajectories. In addition, we study the spectrum of subordinated processes.
- Krapf et al. “Power spectral density of a single Brownian trajectory: what one can and cannot learn from it”, New J. Phys. 20, 023029 (2018)
- Krapf et al., “Spectral content of a single non-Brownian trajectory”, Phys. Rev. X 9, 011019 (2019)
- Fox, Barkai, and Krapf, “Aging power spectrum of membrane protein transport and other subordinated random walks”, Nat. Commun. 12, 6162 (2021)
NANOELECTRODES
We have observed that in nanoelectrodes used in electrochemistry, non-integrable 1/fβ fluctuations appear in the regime where the faradaic currents are governed by mass transport. We exploit these fluctuations to study the impact of reversible adsorption on the transport of charged species. We find that due to a distribution of binding energies, the faradaic currents display weak ergodicity breaking and aging.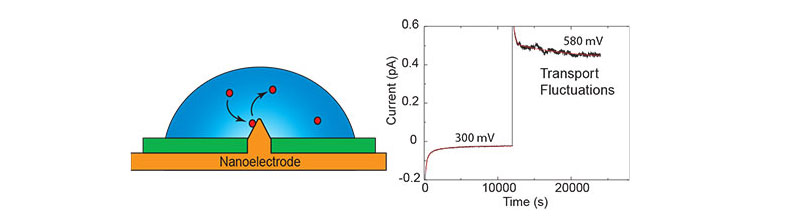
- D. Krapf, “Nonergodicity in nanoscale electrodes“, Phys. Chem. Chem. Phys. 15, 459 (2013)
QUANTUM DOTS
Quantum dots show random transitions between dark and bright states upon continuous excitation, where the residence times in these states follow a power law distribution. Due to their power-law temporal statistics, the emission power spectrum scales as S(f) ~ A/fβ at low frequencies. This type of spectrum is called 1/f noise and it appears in an extensively large array of physical signals. Intriguingly, this type of noise is not integrable in the low-frequency limit.
In our measurements, we observe that as the experimental time increases, the magnitude of the power spectrum is not constant but it decreases. The change of the spectrum with time places a bound on the total power and ensures that the total area under the power spectrum does not blow up. Our work shows that additional critical exponents are needed to fully characterize the dependence of 1/f noise on experimental time.

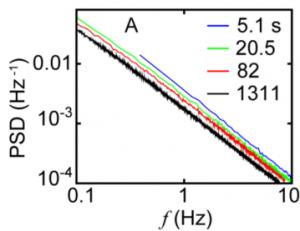
- S. Sadegh, E. Barkai, and D. Krapf, “1/f noise for intermittent quantum dots exhibits non-stationarity and critical exponents“, New J. Phys. 16, 113054 (2014)

Krapf Lab © 2018