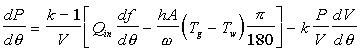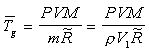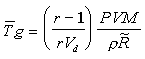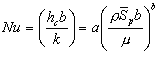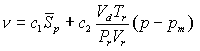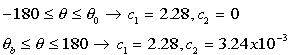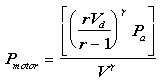Finite Heat Release with Heat Transfer

Introduction
In spark ignition engines, the primary heat transfer mechanism from the cylinder
gases to the wall is convection, with only 5% from radiation.
Using a Newtonian model, the heat loss to the wall is given by:
Q = hA(Tg-Tw)
Where:
-
h = heat transfer coefficient
-
A = exposed combustion chamber surface area
-
Tg = temperature of the cylinder gas
-
Tw = cylinder wall temperature
-
Link to: Finite Heat Release with Heat Transfer Applet
Link to: Heat Transfer Coefficient Applet
Derivation of Pressure versus Crank Angle with the addition
of Heat Transfer
When determining the heat release term,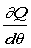 , the heat loss to the walls has to be taken into account. The pressure
over crank angle change now becomes:
, the heat loss to the walls has to be taken into account. The pressure
over crank angle change now becomes:
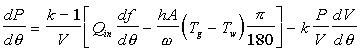
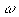 = engine speed [rad/s]
= engine speed [rad/s]
The surface area of the
cylinder can be determined from the slider-crank
model.
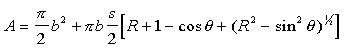 The temperature of the gas, Tg, will be an average temperature.
The temperature will be found from ideal gas relationships.
The temperature of the gas, Tg, will be an average temperature.
The temperature will be found from ideal gas relationships.
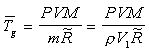 Where:
Where:
M = molar mass of the fuel/air mixture
m = mass of the fuel/air mixture
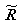 = universal gas constant
= universal gas constant
Using the relationship,
r = V1/V1-Vd:
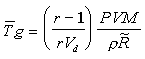
Heat Transfer Coefficient Correlations
Two correlations developed by Annand and Woschni to determine the heat
transfer coefficient will be discussed. The first developed by Annand
is the simpler of the two.
Annand developed the following correlation:
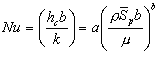 Where:
Where:
hc
= heat transfer coefficient
b
= bore
k
= thermal conductivity =
0.15 W/mK
m
= dynamic viscosity
= 7x105 kg/ms
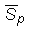 = mean piston speed =
2sw
= mean piston speed =
2sw
a
= varies from 0.35 to 0.8 for normal combustion
b
= 0.7
Woschni accounts for the increase in the gas velocity in the cylinder during
combustion. Annand assumed a constant characteristic gas velocity equal
to the mean piston speed. The average cylinder gas velocity, v,
for a 4-stroke engine without swirl determined by Woschni is:
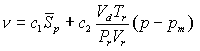
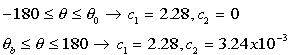 Where:
Where:
-
Pmotor = motor pressure
-
Ta = ambient temperature, 298 K
Pa
= atmospheric pressure, 1 atm
The motoring pressure is given by:
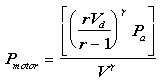
The heat transfer coefficient given by Woschni is:
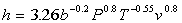
A finite heat release calculation with the Woschni heat transfer model is given in the applet: Finite Heat Release with Heat Transfer Applet. The applet can be used to compare the
effect of adding cylinder heat transfer to the finite heat release model.

![]() , the heat loss to the walls has to be taken into account. The pressure
over crank angle change now becomes:
, the heat loss to the walls has to be taken into account. The pressure
over crank angle change now becomes: