Simple Finite Heat Release Model

Introduction We now account for finite burn duration, in which combustion occurs at

, and continues until

. Figure 6 is a representation of this cycle. The peak pressure will not be as high as the Otto cycle which has a "delta" function heat release. The finite heat release model assumes that the heat input Qin is delivered to the cylinder over a finite crank angle duration.

Heat Release Model

Link to: Heat Release Fraction Applet

Link to: Simple Heat Release Applet

Derivation of Pressure versus Crank Angle for Finite Heat Release

The differential first law for this model for a small crank angle change,

, is:

Using the following definitions,heat release , and , results in :

The ideal gas equation is PV = mRT, so

and

The first law now becomes

Further reducing the equation:

Using R = c_p-c_v and k = c_p/c_v, to define

, the energy equation after rearrangement becomes:

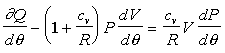
If we know the pressure, P, volume, V, , the heat released gradient, , we can compute the change in pressure, . Thus explicitly solving the equation for pressure as a function of crank angle. Alternatively, we can use experimental data for the pressure, P and the volume, V, to determine the heat release term by solving for .

First, the volume, V and , have to be defined. From the slider-crank model, we have a definition for cylinder volume, V. Both terms are only dependent on engine geometry.

So taking the derivative with respect to the crank angle, , results in :

For heat release term, , the Wiebe function for the burn fraction is used.

Where:

f = the fraction of heat added

= the crank angle

₀ = angle of the start of the heat addition

= the duration of the heat addition (length of burn)

a = usually 5

n = usually 3

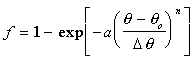
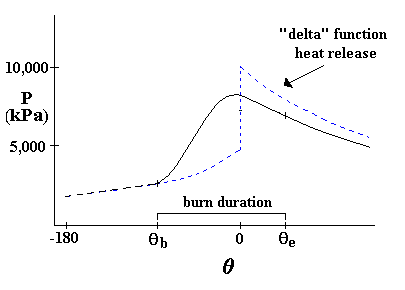
To view the burn fraction, f, as a function of the crank angle, click here: Heat Release Applet.

At the beginning of combustion, f = 0, and at the end the fraction is almost 1.

The heat release, , over the crank angle change, , is:

Where Q_in is the overall heat input.

Taking the derivative of the heat release function, f, with respect to crank angle, gives the following definition of .

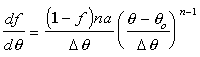
So now with and defined, the pressure as a function of the crank angle can be solved.

The following applet plots the pressure, work and temperature as a function of the crank angle: Simple Heat Release Applet. The effect of heat transfer to the cylinder wall can also be included.

BACK

AHEAD