Chemical Equilibrium
![]()
Introduction
Previously, the products of combustion were determined assuming that the reaction temperature did not reach greater than 1000 K. However the Engine Parameters Performance Applets showed that the reaction temperature does in fact go beyond 1000 K. At these higher temperatures, dissociation of the products occurs. Only the dissociation of carbon dioxide and diatomic nitrogen will be considered. The corresponding reactions are:
![]()
![]()
The reaction can proceed in both directions. The chemical equilibrium constant, K, is defined to described the behavior of the reaction. As K increases, equilibrium for the reaction moves to the right, that is more products are produced. The equilibrium constant for the reverse reaction to the left, is the reciprocal of K for the forward reaction. The equilibrium constant, K, can be related to the partial pressure of the reactants and products. For the following reaction, K is equivalent to:
![]()
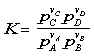
Where:
Partial pressure, pi, is defined as the partial pressure of a component relative to the total pressure. For example, the partial pressure for component A would be:
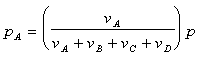
Where p, is the total pressure of the reaction.
Dissociation of Carbon Dioxide
Let's consider the dissociation of carbon dioxide. For the actual case, not all the carbon dioxide would be broken up into carbon monoxide and oxygen. If x is the number of moles of carbon dioxide that dissociate, the reaction can be rewritten as:
![]()
The partial pressures can then be defined as:
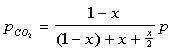
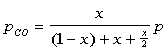
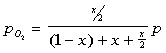
The equilibrium constant can be found to equal the following after some
algebraic manipulation:
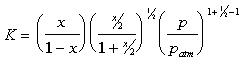
Once K is determined, x can be solved. The equilibrium constant, K, is
a strong function of temperature. As the temperature increases, K increases
as well. The equilibrium constant can be related to the Gibbs function
of the components.
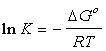
Where :
The Gibb function is equivalent to:
![]()
![]()
Values for K have been tabulated for several reactions at various temperatures. These values come from the above relations, which are determined by statical thermodynamics. The process is much to drawn out to go into a derivation here. For further explanation see , Fundamentals of Statistical Thermodynamics, by R.E. Sonntag and G.J. Van Wylen, chapter eleven.
The following applet determined the resulting molar and mass composition of the products based on the reaction temperature and pressure. Click here to view the applet: Dissociation of CO2.
Dissociation of Diatomic Nitrogen
The same procedure can be followed to determine the molar amounts for the dissociation of diatomic nitrogen to nitrous oxide, NO. The actual reaction is given by:
![]()
The partial pressure are:
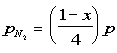
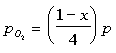
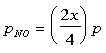
The equilibrium constant can be determined to be equal to:
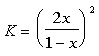
Where x can be easily solved for:
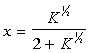
This second applet determines the molar and mass quantities of the products: Dissociation of Diatomic Nitrogen.
![]()
 |
 |