Even genetically identical cells in identical environments exhibit wildly different phenotypical behaviors due to cellular fluctuations known as gene expression "noise". In fact, our recent work shows that even individual mRNA molecules within the same cell can randomly fluctuate between "molecular phenotypes", such as stochastic periods (or "bursts") in canonical and non-canonical translation. Previously, cellular noise was considered a nuisance that compromised cellular responses, complicated modeling, and made predictive understanding all but impossible. Early studies focused on how cellular processes could remove or exploit noise to a cell's advantage. By integrating new experiments and models, we can now show that different cellular mechanisms affect cellular and molecular fluctuations in different ways, and it is now clear that these fluctuations encode valuable information about underlying mechanisms. Our research uses statistical analyses to discover unique "fluctuation fingerprints" in single-cell and single-molecule data, machine learning and Bayesian analyses to find and quantify uncertainty in data-driven models, and computer aided experiment design to squeeze every bit of information possible out of every research dollar. Through these efforts we have been able to uncover precise, quantitative, and predictive understanding of natural and synthetic transcriptional regulation pathways in bacteria, yeast and mammalian cells at scales ranging from activation of a single gene or mRNA molecule to the interactions between thousands of species in a soil microbial community.
Curr_Proj.
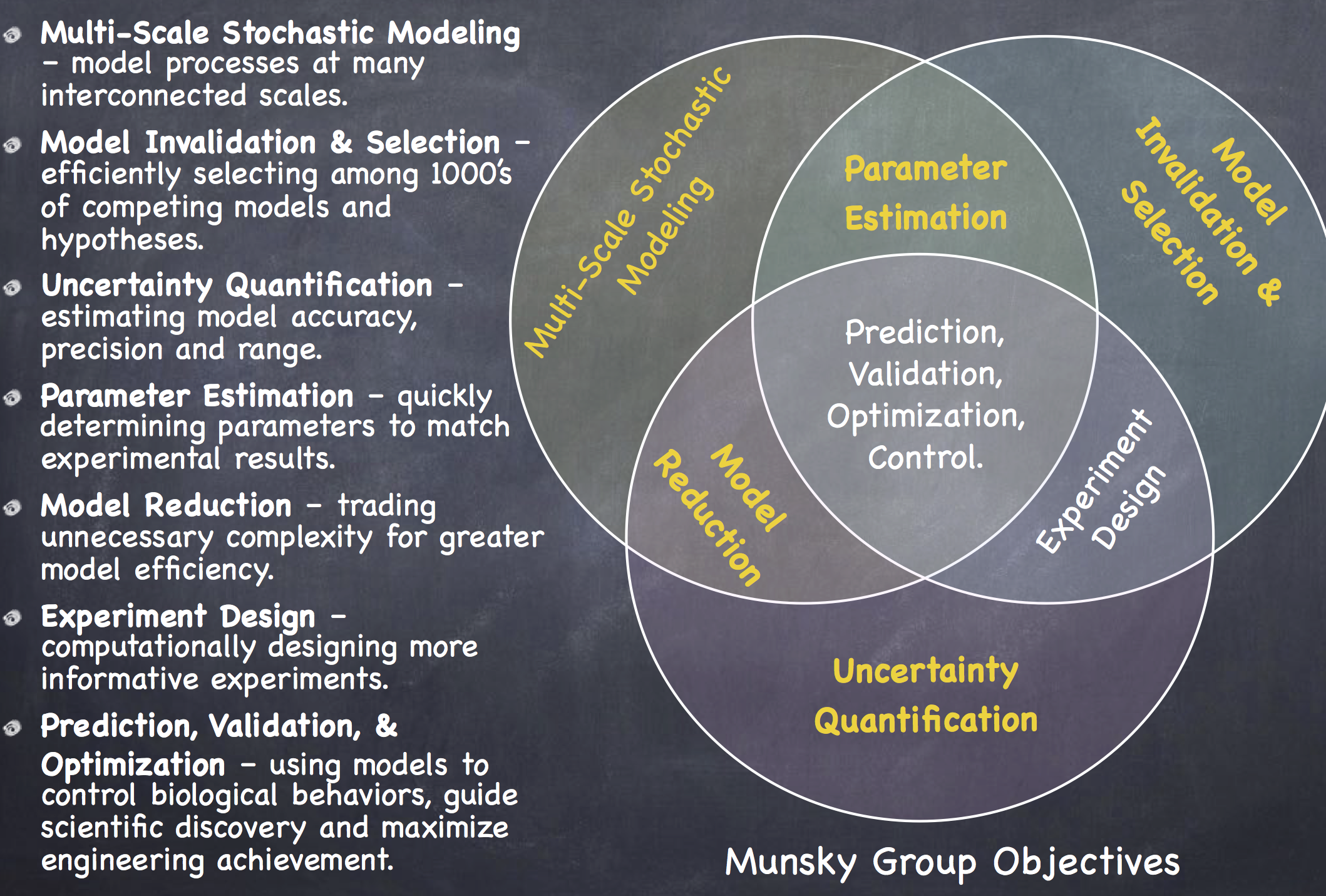
Current Projects
Emerging techniques now allow for precise quantification of distributions of biological molecules in single cells. These rapidly advancing experimental methods have created a need for more rigorous and efficient modeling tools. Many of the tools we use are extensions of the Finite State Projection approach, which allows us to compute the precise time-varying probability distributions of single-cell responses, even in fluctuating environments.
New Bounds on Likelihoods of Single-Cell Data.
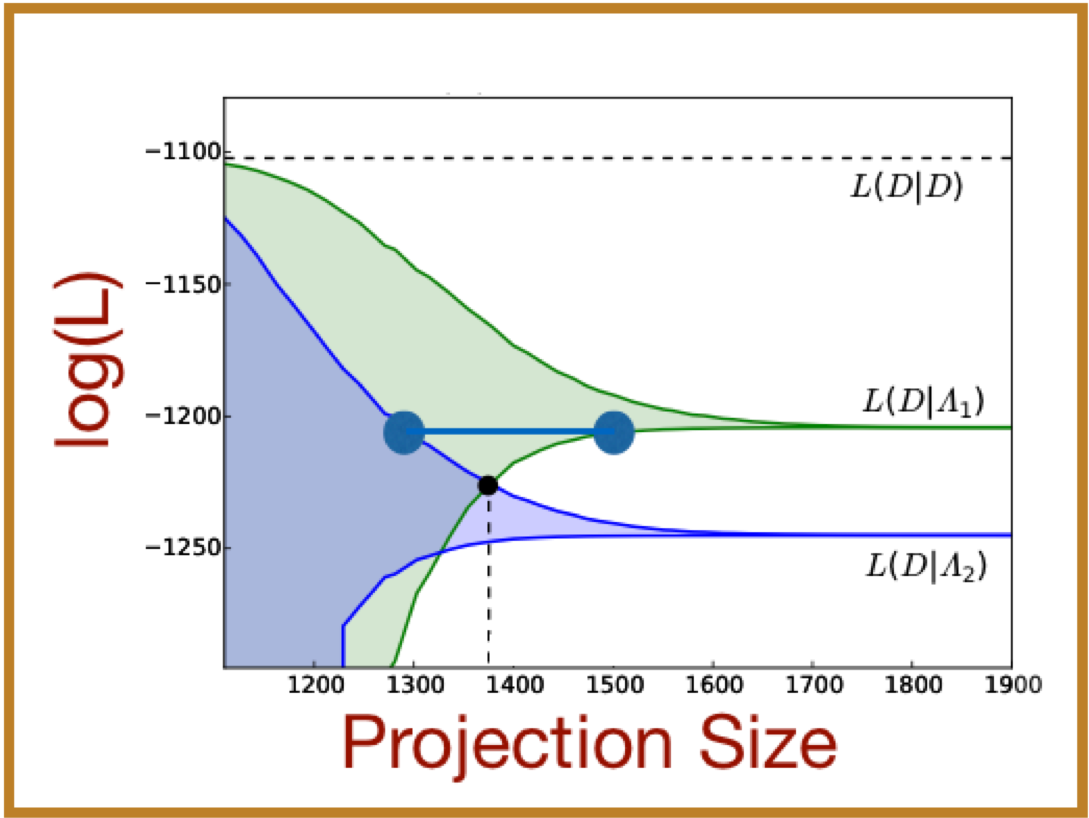
We have recently derived new bounds on the likelihood that observations of single-cell, single-molecule responses come from a discrete stochastic model, which we pose in the form of the chemical master equation (CME). These strict upper and lower bounds are based on a technique known as the Finite State Projection, and they converge monotonically to the exact likelihood value. By calculating these bounds, we can rigorously discriminate between models with a minimum level of computational effort. In practice, we have incorporated these FSP-derived likelihood bounds bounds into stochastic model identification and parameter inference routines, which improve the accuracy and efficiency of endeavors to analyze and predict single-cell behavior. We have demonstrated the applicability of our approach using simulated data for multiple models with simulated data as well as for experimental measurements of a time-varying stochastic transcriptional response in yeast.
[1] Z. Fox, G. Neuert and B. Munsky, Finite state projection based bounds to compare chemical master equation models using single-cell data, Journal of Chemical Physics, 145:7, 074101 (2016), online here
Estimating and maximizing the information in single-cell experiments.
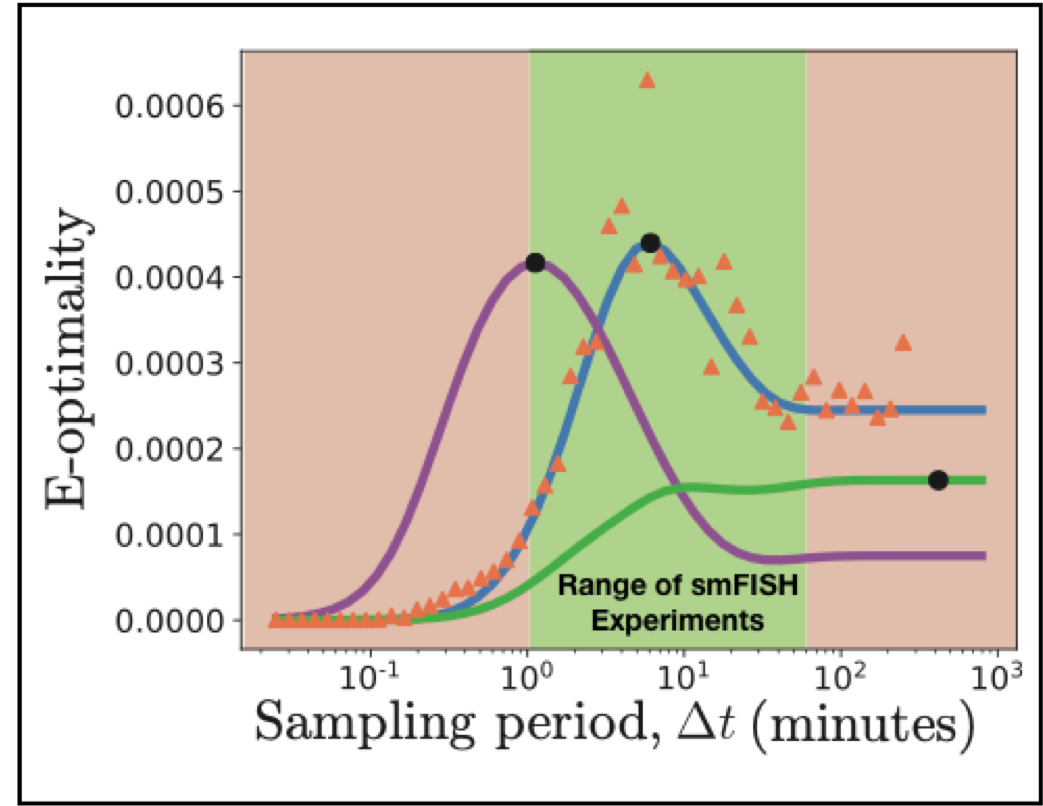 Modern experiments not only measure single-cell and single-molecule dynamics with high precision, but they can also perturb the cellular environment in myriad controlled and novel settings. Such techniques have opened the door to an infinite number of potential experiments, which begs the question of how best to choose the next experiment. The Fisher information matrix (FIM) estimates how well potential experiments will constrain model parameters and can be used to design optimal experiments. Here, we introduce the finite state projection (FSP) based FIM, which uses the formalism of the chemical master equation to derive and compute the FIM. The FSP-FIM makes no assumptions about the distribution shapes of single-cell data, and it does not require precise measurements of higher order moments of such distributions. We validate the FSP-FIM against well-known Fisher information results for the simple case of constitutive gene expression. We then demonstrate the use of the FSP-FIM to optimize the timing of single-cell experiments with more complex, non-Gaussian fluctuations. We validate optimal experiments determined using the FSP-FIM with Monte-Carlo approaches and contrast these to experiments chosen by traditional analyses that assume Gaussian fluctuations or use the central limit theorem. By systematically designing experiments to use all of the measurable fluctuation information, our method enables a key step to improve co-design of experiments and quantitative models.
Modern experiments not only measure single-cell and single-molecule dynamics with high precision, but they can also perturb the cellular environment in myriad controlled and novel settings. Such techniques have opened the door to an infinite number of potential experiments, which begs the question of how best to choose the next experiment. The Fisher information matrix (FIM) estimates how well potential experiments will constrain model parameters and can be used to design optimal experiments. Here, we introduce the finite state projection (FSP) based FIM, which uses the formalism of the chemical master equation to derive and compute the FIM. The FSP-FIM makes no assumptions about the distribution shapes of single-cell data, and it does not require precise measurements of higher order moments of such distributions. We validate the FSP-FIM against well-known Fisher information results for the simple case of constitutive gene expression. We then demonstrate the use of the FSP-FIM to optimize the timing of single-cell experiments with more complex, non-Gaussian fluctuations. We validate optimal experiments determined using the FSP-FIM with Monte-Carlo approaches and contrast these to experiments chosen by traditional analyses that assume Gaussian fluctuations or use the central limit theorem. By systematically designing experiments to use all of the measurable fluctuation information, our method enables a key step to improve co-design of experiments and quantitative models.
[2] ZR Fox and B. Munsky, The finite state projection based Fisher information matrix approach to estimate information and optimize single-cell experiments, PLoS computational biology 15 (1), e1006365, online here
[3] ZR Fox, G Neuert, B. Munsky, Optimal Design of Single-Cell Experiments within Temporally Fluctuating Environments, Complexity 2020, online here
Bayesian estimation for stochastic gene expression using multifidelity models
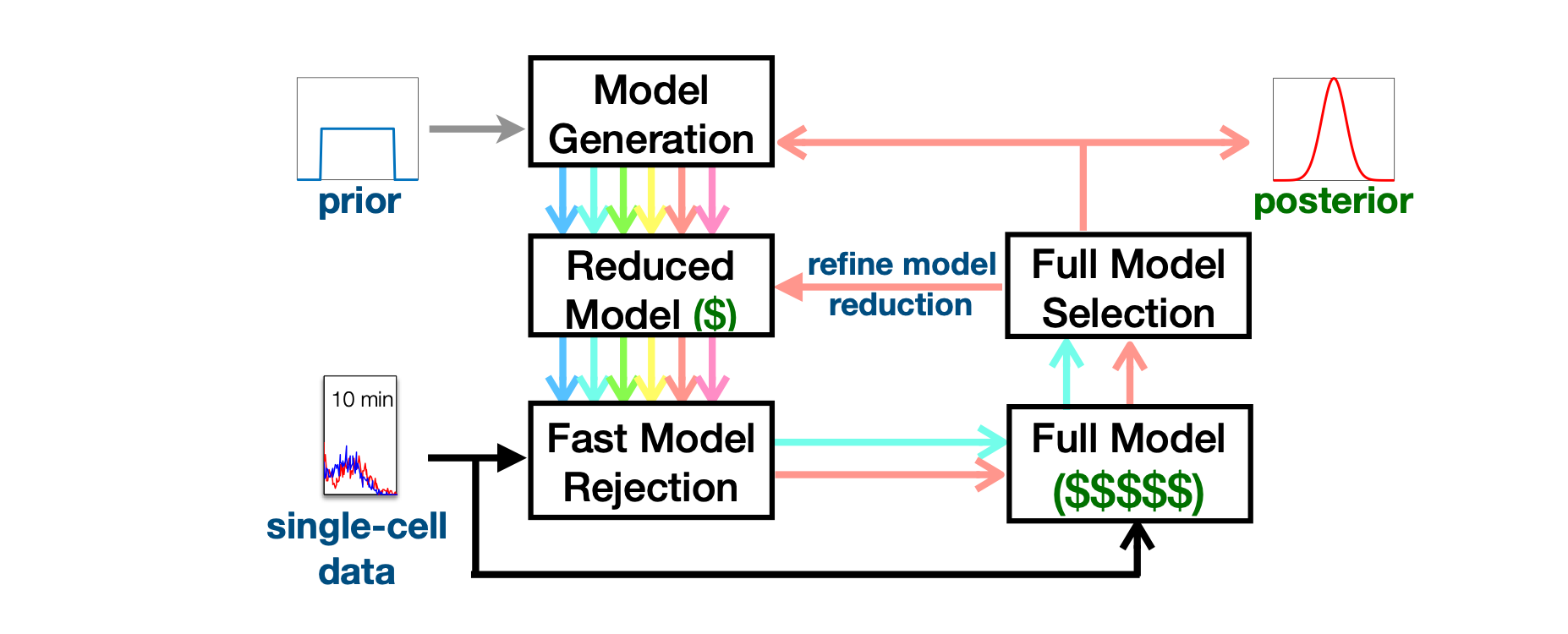 The finite state projection (FSP) approach to solving the chemical master equation (CME) has enabled successful inference of discrete stochastic models to predict single-cell gene regulation dynamics. Unfortunately, the FSP approach is highly computationally intensive for all but the simplest models, an issue that is highly problematic when parameter inference and uncertainty quantification takes enormous numbers of parameter evaluations. To address this issue, we propose two new computational methods for the Bayesian inference of stochastic gene expression parameters given single-cell experiments. First, we present an adaptive scheme to improve parameter proposals for Metropolis-Hastings sampling using full FSP-based likelihood evaluations. We then formulate and verify an Adaptive Delayed Acceptance Metropolis-Hastings (ADAMH) algorithm to utilize with reduced Krylov-basis projections of the FSP. We test and compare both algorithms on three example models and simulated data to show that the ADAMH scheme achieves substantial speedup in comparison to the full FSP approach. By reducing the computational costs of parameter estimation, we expect the ADAMH approach to enable efficient data-driven estimation for more complex gene regulation models.
The finite state projection (FSP) approach to solving the chemical master equation (CME) has enabled successful inference of discrete stochastic models to predict single-cell gene regulation dynamics. Unfortunately, the FSP approach is highly computationally intensive for all but the simplest models, an issue that is highly problematic when parameter inference and uncertainty quantification takes enormous numbers of parameter evaluations. To address this issue, we propose two new computational methods for the Bayesian inference of stochastic gene expression parameters given single-cell experiments. First, we present an adaptive scheme to improve parameter proposals for Metropolis-Hastings sampling using full FSP-based likelihood evaluations. We then formulate and verify an Adaptive Delayed Acceptance Metropolis-Hastings (ADAMH) algorithm to utilize with reduced Krylov-basis projections of the FSP. We test and compare both algorithms on three example models and simulated data to show that the ADAMH scheme achieves substantial speedup in comparison to the full FSP approach. By reducing the computational costs of parameter estimation, we expect the ADAMH approach to enable efficient data-driven estimation for more complex gene regulation models.
[5] H D. Vo, Z Fox, A Baetica and B Munsky, Bayesian Estimation for Stochastic Gene Expression Using Multifidelity Models, J. Phys. Chem. B, 2019, 123 (10), pp 2217–2234, online here.
[6] T.A. Catanach, H.D. Vo, B. Munsky, Bayesian inference of Stochastic reaction networks using Multifidelity Sequential Tempered Markov Chain Monte Carlo, arXiv:2001.01373, 2020, online here.
CSU Students and Postdocs:
Zachary Fox (PhD Student, graduated June, 2019). Now at Los Alamos National Laboratory.
Huy Vo (Postdoc, 2017-present)
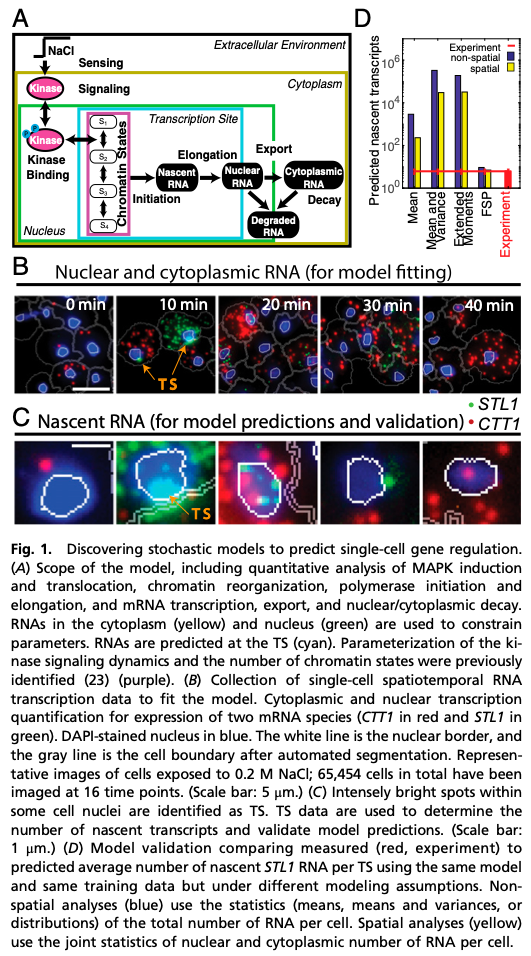 When biological models under-perform expectations, it is tempting to attribute failure to “bad models” or “insufficient data”. However, predictions from good models and sufficient data may fail due to poor integration of the two. Unlike most engineered systems, biological fluctuations are dominated by discrete fluctuations in DNA, RNA and protein. Integrating stochastic models with single-cell experiments can provide a wealth of information about gene regulatory dynamics [1], but for discrete, positive fluctuations, standard data-model integration analyses (e.g., assuming normal distributions or making CLT arguments) can produce nearly perfect fits to old data yet fail dramatically to predict new phenomena. Yet, when these fail, approaches that dispense with CLT assumptions can yield extremely accurate quantitative predictions, even for the exact same data and exact same models.
When biological models under-perform expectations, it is tempting to attribute failure to “bad models” or “insufficient data”. However, predictions from good models and sufficient data may fail due to poor integration of the two. Unlike most engineered systems, biological fluctuations are dominated by discrete fluctuations in DNA, RNA and protein. Integrating stochastic models with single-cell experiments can provide a wealth of information about gene regulatory dynamics [1], but for discrete, positive fluctuations, standard data-model integration analyses (e.g., assuming normal distributions or making CLT arguments) can produce nearly perfect fits to old data yet fail dramatically to predict new phenomena. Yet, when these fail, approaches that dispense with CLT assumptions can yield extremely accurate quantitative predictions, even for the exact same data and exact same models.
We are demonstrating these crucial model-data integration concerns using single-cell-single-molecule data collected on an evolutionarily conserved Mitogen-Activated Protein Kinase (MAPK) pathway and its downstream induction of mRNA transcription in yeast. We discuss how different modeling assumptions affect parameter uncertainties or bias and how these errors affect predictive understanding.
We examine the stress response High Osmolarity Glycerol (Hog1) pathway and its control of transcription mechanisms (polymerase initiation and elongation, mRNA export, and accumulation and degradation) during transient adaptation to hyper-osmotic shock. Our collaborators in the Neuert Lab at Vanderbilt University have quantified individual mRNA at the site of transcription, in the nucleus, and in the cytoplasm for multiple genes using single-molecule fluorescence hybridization for more than 65,000 cells at many points in time, different environmental conditions, and in multiple replica experiments. These measured distributions are demonstrably non-normal and non-symmetric, which has important implications on the results of model-data integration.
We extend a multi-state gene expression model [1,2] to account for transcriptional regulation and spatial localization of mRNA. We solve this model with three exact computational methods: (1) a deterministic ODE analysis, (2) a linear noise analysis, and (3) a chemical master equation (CME) solution. We invoke the CLT to approximate the likelihood of all data given the model for analyses (1)&(2), and we compute the exact likelihood using analysis (3). For each case, we use Metropolis Hastings sampling to find the maximum likelihood and posterior distribution of the parameters, given the data.
Despite excellent fits to training data, the CLT-methods fail to predict the full statistics, and parameter uncertainty and bias errors in the CLT-approaches are orders of magnitude larger than for the CME-approach. Use of second moments (i.e., (co)variances) modestly reduces uncertainty, but exacerbates the bias and yields even worse predictions. We trace this effect to asymmetry in the RNA distributions, which causes systematic under-estimation of the moments and leads CLT-approaches to overestimate RNA degradation rates by multiple orders of magnitude compared to results in different yeast strains [2]. In contrast, the CME-approach recovers these rates within 5-8%, indicating strong repeatability of both experiments and analyses.
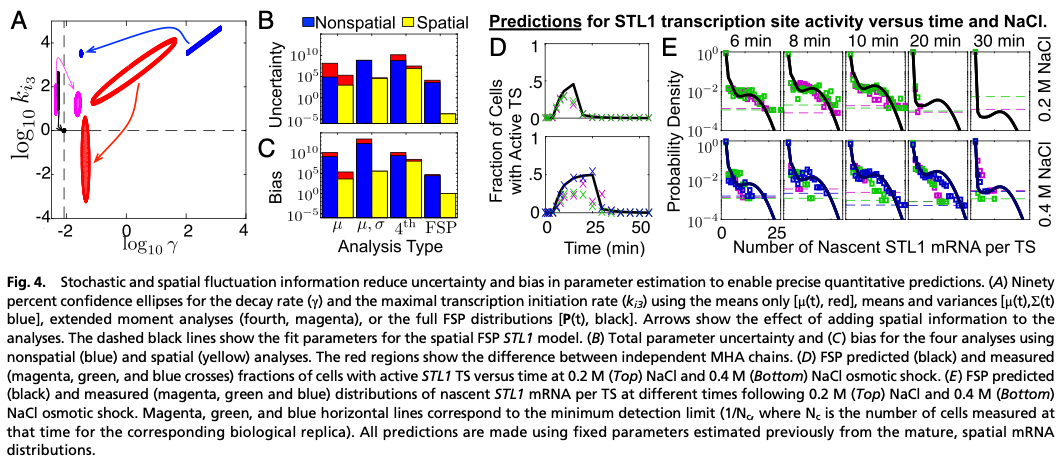 We used the identified models to predict the elongation dynamics of nascent mRNA at transcription sites (TS). Using TS images for endogenous mRNA for the CTT1 gene, we estimated Pol II elongation rate in excelent agreement with published rates. Using no additional free parameters, we correctly predicted and then measured (i) the average full-length STL1 mRNA per active TS, (ii) the quantitative fraction of cells that have active TS’s versus time, and (iii) the full distributions of nascent mRNA (or equivalently the number of associated elongating Pol II) per TS.
We used the identified models to predict the elongation dynamics of nascent mRNA at transcription sites (TS). Using TS images for endogenous mRNA for the CTT1 gene, we estimated Pol II elongation rate in excelent agreement with published rates. Using no additional free parameters, we correctly predicted and then measured (i) the average full-length STL1 mRNA per active TS, (ii) the quantitative fraction of cells that have active TS’s versus time, and (iii) the full distributions of nascent mRNA (or equivalently the number of associated elongating Pol II) per TS.
CSU Students and Postdocs:
Zachary Fox (PhD Student, graduated May 2019). Now at Los Alamos National Laboratory
Joshua Cook (Undergrad)
Huy Vo (Postdoc)
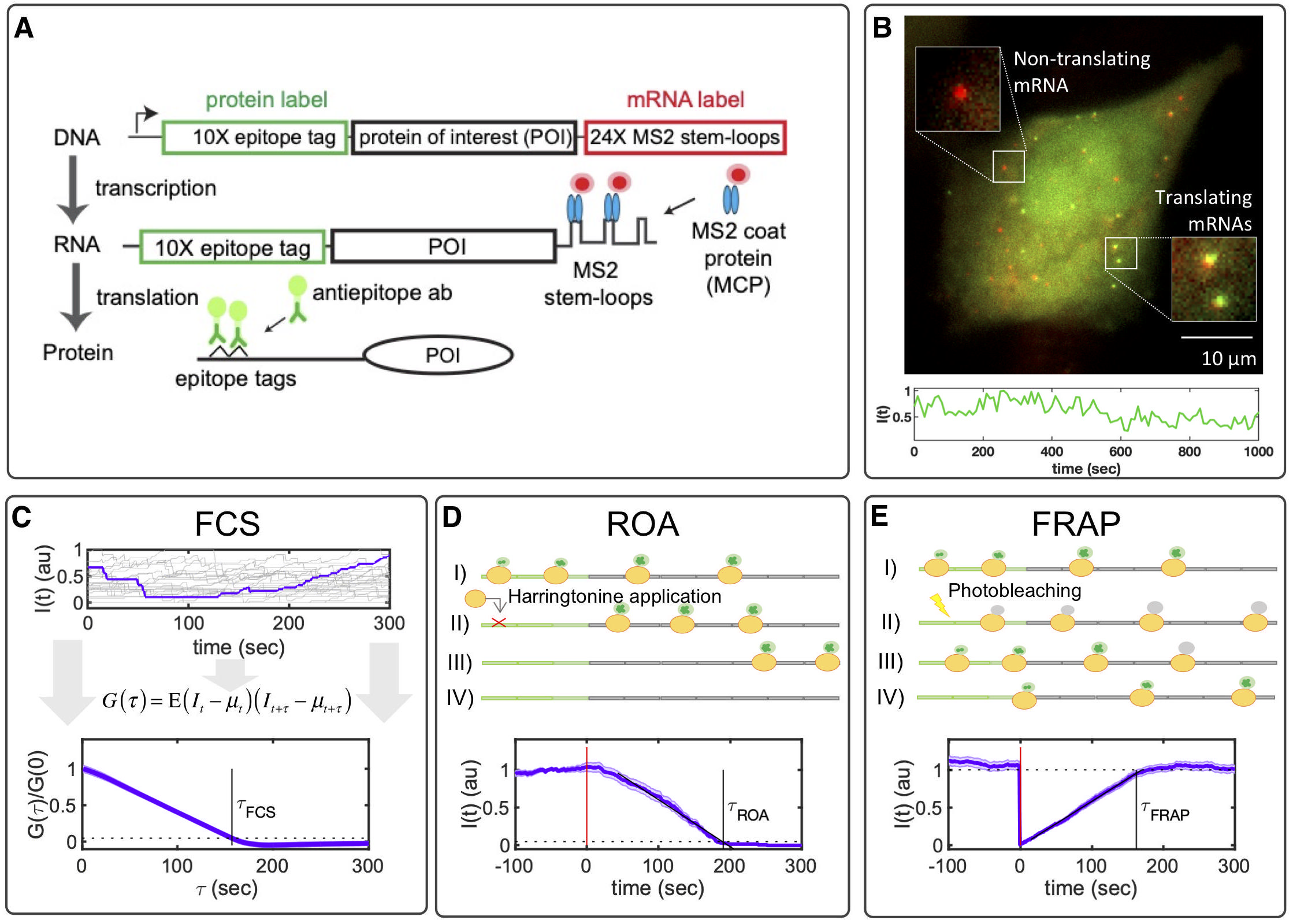
Translation is an essential step in which ribosomes decipher mRNA sequences to manufacture proteins. Recent advances in single-molecule imaging allow live-cell quantification of the kinetics of ribosome initiation and elongation (Panels A,B). First, we use MS2/MCP to tag the 3' region of mRNA molecules in red. Then, we place a number of epitope tags in the 5' region of the mRNA, which are recognized and bound by fluorescent antibody fragments in green. Now that we have fluorescent reporters of nascent protein translation, we can use different experimental approaches to estimate key parameters of single-mRNA translation (Panel C), including fluorescence correlation spectroscopy (FCS), run off assays (ROA) or fluorescence recovery after photo-bleaching (FRAP).
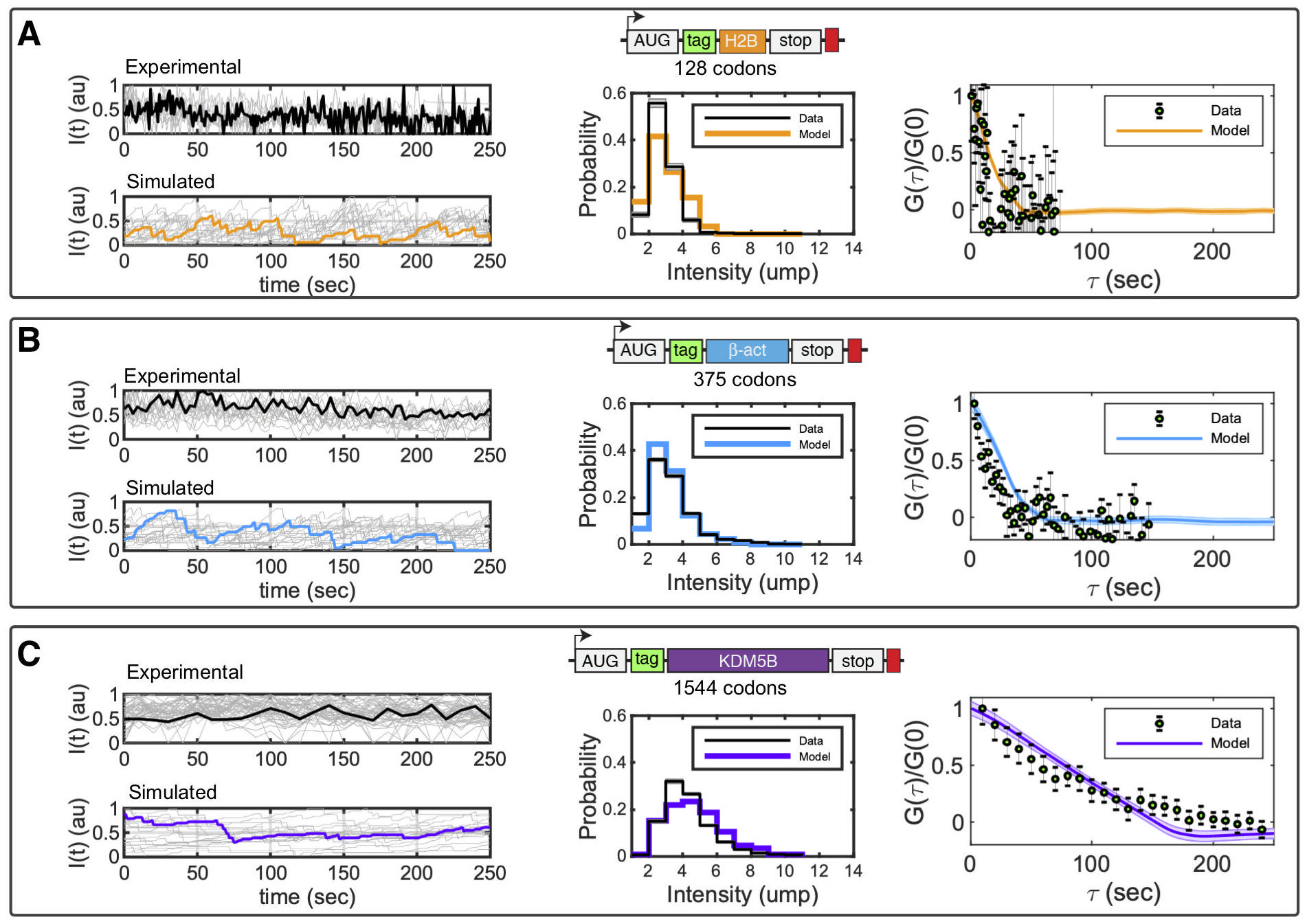 New computational tools to predict codon-dependent translation fluctuation dynamics. We integrate single-molecule data and stochastic models to investigate how elongation rates vary among different gene transcripts. Our computational method automatically generates discrete translation models to match any mRNA sequence. The models are then solved using stochastic dynamics; the results are quantified in terms of translation spot intensity; and we fit these data collected from single-mRNA translating spots observed under the microscope -- for multiple different genes (Panels A-C). With our new computational analyses, we are poised to compare models with different codon-dependent elongation rates; to simulate the effect of chemical perturbations, puromycin and harringtonine, which inhibit elongation and initiation steps, respectively. Because codon usage and chemical environments both effect translation mechanisms, our integrated models and single-mRNA measurements allow us to extract the kinetics of protein production and to infer how these kinetics are controlled by cellular states and mRNA sequences.
New computational tools to predict codon-dependent translation fluctuation dynamics. We integrate single-molecule data and stochastic models to investigate how elongation rates vary among different gene transcripts. Our computational method automatically generates discrete translation models to match any mRNA sequence. The models are then solved using stochastic dynamics; the results are quantified in terms of translation spot intensity; and we fit these data collected from single-mRNA translating spots observed under the microscope -- for multiple different genes (Panels A-C). With our new computational analyses, we are poised to compare models with different codon-dependent elongation rates; to simulate the effect of chemical perturbations, puromycin and harringtonine, which inhibit elongation and initiation steps, respectively. Because codon usage and chemical environments both effect translation mechanisms, our integrated models and single-mRNA measurements allow us to extract the kinetics of protein production and to infer how these kinetics are controlled by cellular states and mRNA sequences.
Manuscripts:
- L. Aguilera, W. Raymond, Z. R. Fox, M. P. May, E. Djokic, T. Morisaki, T. J. Stasevich, B. Munsky, Computational design and interpretation of live-cell, single-RNA translation experiments, PLoS Computational Biology, 15(10): e1007425, online here
- rna Sequence to NAscent Protein simulator (rSNAPsim): https://github.com/MunskyGroup/rSNAPsim
Real time, single-mRNA quantification of translational frameshifting. Ribosomal frameshifting during the translation of RNA is implicated in both human disease and viral infection. While previous work has uncovered many mechanistic details about single RNA frameshifting kinetics in vitro, very little is known about how single RNA frameshift in living systems. To confront this problem, we have developed technology to quantify live-cell single RNA translation dynamics in frameshifted open reading frames. Applying this technology to RNA encoding the HIV-1 frameshift sequence reveals a small subset (~8%) of the translating pool robustly frameshift in living cells. Frameshifting RNA are preferentially in multi-RNA 9translation factories,9 are translated at about the same rate as non-frameshifting RNA (~2 aa/sec), and can continuously frameshift for more than four rounds of translation. Fits to a bursty model of frameshifting constrain frameshifting kinetic rates and demonstrate how ribosomal traffic jams contribute to the persistence of the frameshifting state. These data provide novel insight into retroviral frameshifting and could lead to new strategies to perturb the process in living cells.
- K R Lyon Jr., L U Aguilera, T Morisaki, B Munsky, T J Stasevich, Live-cell single RNA imaging reveals bursts of translational frameshifting, Molecular Cell, 7:1, 2019, online here
- A L Koch, L Aguilera, T Morisaki, B E Munsky, T J Stasevich, Quantifying the spatiotemporal dynamics of IRES versus Cap translation with single-molecule resolution in living cells, Nat Struct Mol Biol, 27:12, 2020 online here
CSU Students:
Ken Lyon (PhD student in Tim Stasevich Lab, Postdoc in Munsky Lab, now at University of Utah)
Luis Aguilera (Postdoc in Munsky Lab)
Microbial communities are ubiquitous and often influence macroscopic properties of the ecosystems they inhabit. However, deciphering the functional relationship between specific microbes and ecosystem properties is an ongoing challenge owing to the complexity of the communities. This challenge can be addressed, in part, by integrating the advances in DNA sequencing technology with computational approaches like machine learning. Although machine learning techniques have been applied to microbiome data, use of these techniques remains rare, and user-friendly platforms to implement such techniques are not widely available.
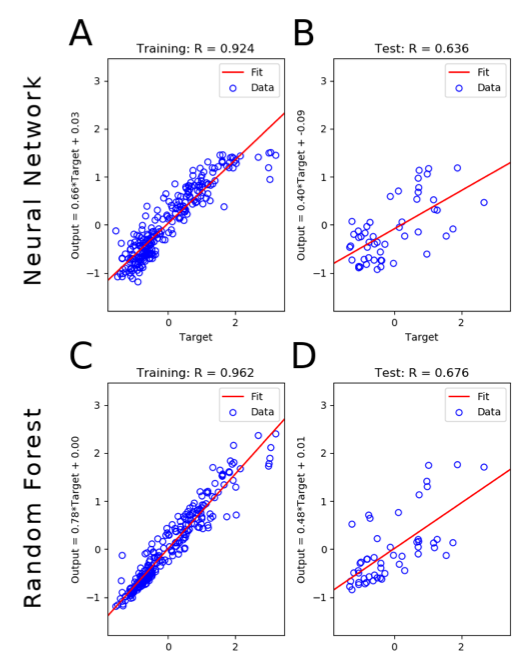 We developed a tool that implements neural network and random forest models to perform regression and feature selection tasks on microbiome data. In this study, we applied the tool to analyze soil microbiome (16S rRNA gene profiles) and dissolved organic carbon (DOC) data from a 45-day plant litter decomposition experiment. The microbiome data includes 1709 total bacterial operational taxonomic units from 300+ microcosms. Regression analysis of predicted and actual DOC for a held-out test set of 51 samples yield Pearson's correlation coefficients of 0.636 and 0.676 for neural network and random forest approaches, respectively. Important taxa identified by the machine learning techniques are compared to results from a standard tool (indicator species analysis) widely used by microbial ecologists. Of 1709 bacterial taxa, indicator species analysis identified 285 taxa as significant determinants of DOC concentration. Of the top 285 ranked features determined by machine learning methods, a subset of 86 taxa are common to all feature selection techniques. Using this subset of features, prediction results for random permutations of the data set are at least equally accurate compared to predictions determined using the entire feature set. Our results suggest that integration of multiple methods can aid identification of a robust subset of taxa within complex communities that may drive specific functional outcomes of interest.
We developed a tool that implements neural network and random forest models to perform regression and feature selection tasks on microbiome data. In this study, we applied the tool to analyze soil microbiome (16S rRNA gene profiles) and dissolved organic carbon (DOC) data from a 45-day plant litter decomposition experiment. The microbiome data includes 1709 total bacterial operational taxonomic units from 300+ microcosms. Regression analysis of predicted and actual DOC for a held-out test set of 51 samples yield Pearson's correlation coefficients of 0.636 and 0.676 for neural network and random forest approaches, respectively. Important taxa identified by the machine learning techniques are compared to results from a standard tool (indicator species analysis) widely used by microbial ecologists. Of 1709 bacterial taxa, indicator species analysis identified 285 taxa as significant determinants of DOC concentration. Of the top 285 ranked features determined by machine learning methods, a subset of 86 taxa are common to all feature selection techniques. Using this subset of features, prediction results for random permutations of the data set are at least equally accurate compared to predictions determined using the entire feature set. Our results suggest that integration of multiple methods can aid identification of a robust subset of taxa within complex communities that may drive specific functional outcomes of interest.
This research is being performed in collaboration with experimental efforts in John Dunbar's laboratory at Los Alamos National Laboratory.
Manuscripts:
- J. Thompson, R. Johansen, J Dunbar, B Munsky, Machine learning to predict microbial community functions: An analysis of dissolved organic carbon from litter decomposition, PLoS One, 14(7): e0215502, 2019, online here.
- J Thompson, N Lubbers, M E Kroeger, R DeVan, R Johansen, J Dunbar, B Munsky, Probabilistic Ranking Of Microbiomes Plus Taxa Selection to discover and validate microbiome function models for multiple litter decomposition studies, bioRxiv, 2020, online here
- M B. N. Albright, R Johansen, J Thompson, D Lopez, LV Gallegos-Graves, M Kroeger, A Runde, R C Mueller, A Washburne, B Munsky, T Yoshida, J Dunbar, Soil bacterial and fungal richness forecast patterns of early pine litter decomposition, Frontiers in Microbiology, section Terrestrial Microbiology, in press, 2020, online here
- M B N Albright, J Thompson, M E Kroeger, R Johansen, D E M Ulrich, LV Gallegos-Graves, B Munsky, J Dunbar, Differences in substrate use linked to divergent carbon flow during litter decomposition, FEMS Microbiology Ecology, fiaa135, 2020, online here
CSU Students:
Jaron Thompson (MS, anticipated graduation May 2020).
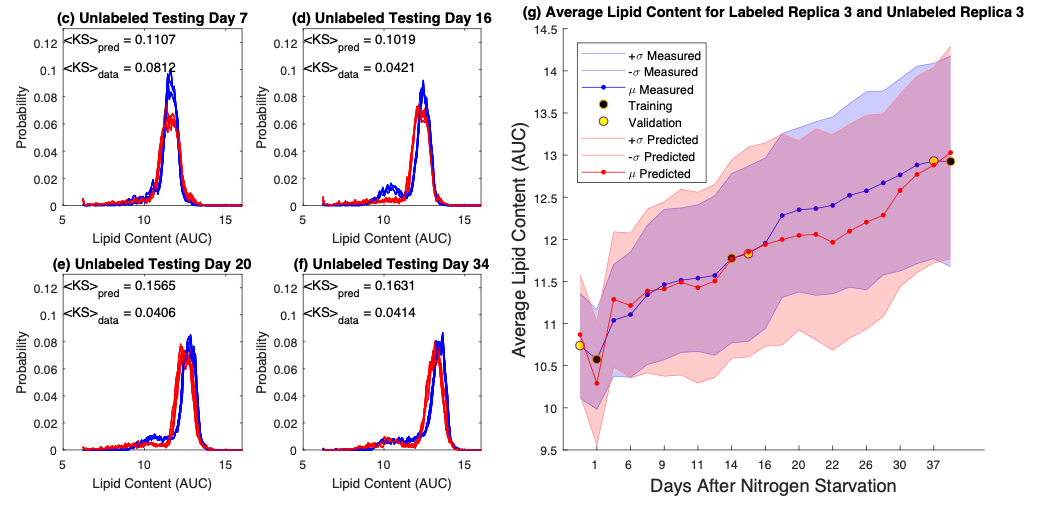
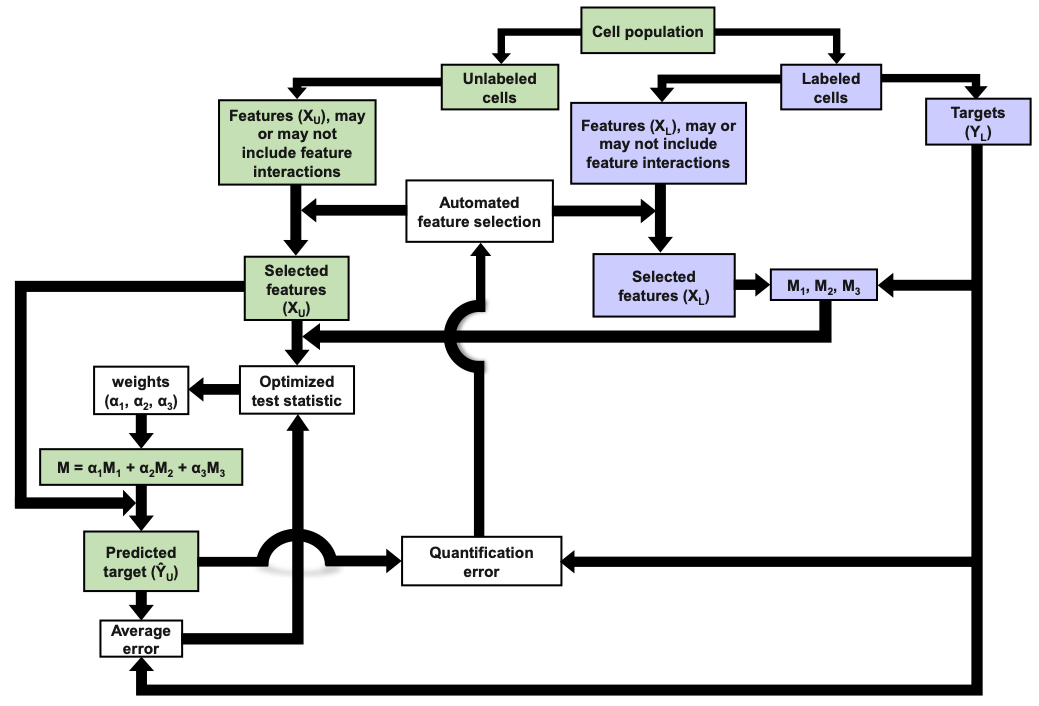 Flow cytometry typically relies upon specific biochemical labels, though they are not always available, they can be costly, and they can disrupt natural cell behavior. Label-free quantification strategies are needed to correct these issues. Unfortunately, label replacement strategies may be difficult to learn if applied labels or other modifications in training data inadvertently modify intrinsic cell properties. Here we demonstrate development of a new approach based upon population statistics and machine learning to integrate labeled and unlabeled training data and to identify models for accurate label-free quantification. Accuracy of this method is then shown by evaluating the resulting ability of the machine learning approach to quantify lipid content in new conditions as part of an algal biofuel application. We apply our approach to make and test label-free quantification of lipid content in Picochlorum sp., at multiple times following nitrogen starvation and lipid accumulation.
Flow cytometry typically relies upon specific biochemical labels, though they are not always available, they can be costly, and they can disrupt natural cell behavior. Label-free quantification strategies are needed to correct these issues. Unfortunately, label replacement strategies may be difficult to learn if applied labels or other modifications in training data inadvertently modify intrinsic cell properties. Here we demonstrate development of a new approach based upon population statistics and machine learning to integrate labeled and unlabeled training data and to identify models for accurate label-free quantification. Accuracy of this method is then shown by evaluating the resulting ability of the machine learning approach to quantify lipid content in new conditions as part of an algal biofuel application. We apply our approach to make and test label-free quantification of lipid content in Picochlorum sp., at multiple times following nitrogen starvation and lipid accumulation.
This research is being performed in collaboration with experimental efforts in Babetta Marrone's laboratory at Los Alamos National Laboratory.
Manuscripts:
M Tanhaemami, E Alizadeh, C Sanders, B Marrone, B Munsky, Using Flow Cytometry and Multistage Machine Learning to Discover Label-Free Signatures of Algal Lipid Accumulation, Physical Biology, 16:5, 2019, online here
CSU Students:
Mohammad Tanhaemami (MS, graduation May 2019).
One of the many ways that bacteria use to evade antibiotic treatments is Bacterial Persistence. In this phenomena, rare cells in a large population transiently enter into a dormant state in which they do not grow, but they are also not responsive to antibiotics in their environment. these cells can later escape their dormant state to replenish the population after antibiotics are cleared from the environment. We are interested to develop quantitative models for the epigenetic heterogeneity of persistence in the context of time varying environments. If we can predict what circumstances lead to persistence, we can use these to design more effective control strategies to maximize the effectiveness of antibiotics while minimizing the time and amount of treatments.
New Computational Approaches to Model Heterogenous Populations.
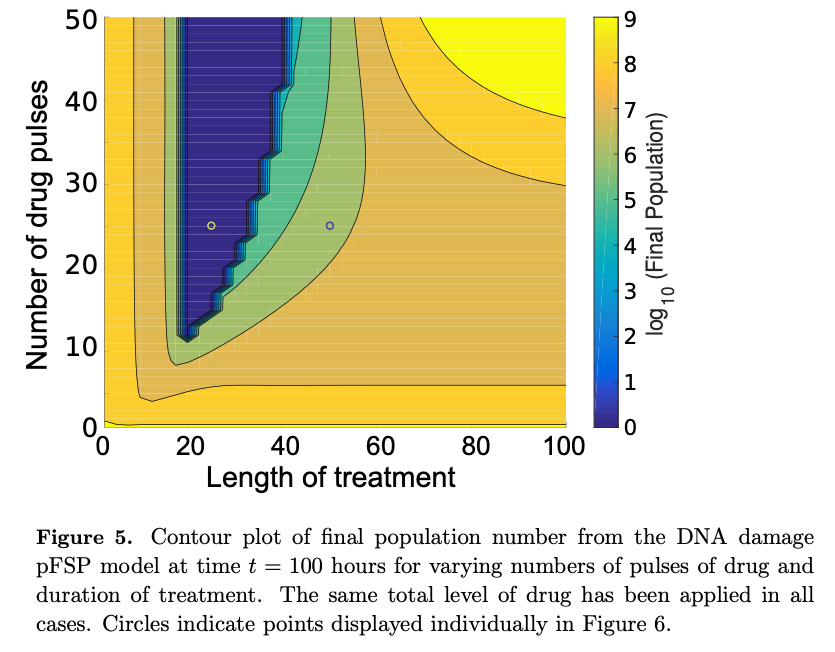 Population modeling aims to capture and predict the dynamics of cell populations in constant or fluctuating environments. At the elementary level, population growth proceeds through sequential divisions of individual cells. Due to stochastic effects, populations of cells are inherently heterogeneous in phenotype, and some phenotypic variables have an effect on division or survival rates, as can be seen in partial drug resistance. Therefore, when modeling population dynamics where the control of growth and division is phenotype dependent, the corresponding model must take account of the underlying cellular heterogeneity. The finite state projection (FSP) approach has often been used to analyze the statistics of independent cells. Here, we extend the FSP analysis to explore the coupling of cell dynamics and biomolecule dynamics within a population. This extension allows a general framework with which to model the state occupations of a heterogeneous, isogenic population of dividing and expiring cells. The method is demonstrated with a simple model of cell-cycle progression, which we use to explore possible dynamics of drug resistance phenotypes in dividing cells. We use this method to show how stochastic single-cell behaviors affect population level efficacy of drug treatments, and we illustrate how slight modifications to treatment regimens may have dramatic effects on drug efficacy.
Population modeling aims to capture and predict the dynamics of cell populations in constant or fluctuating environments. At the elementary level, population growth proceeds through sequential divisions of individual cells. Due to stochastic effects, populations of cells are inherently heterogeneous in phenotype, and some phenotypic variables have an effect on division or survival rates, as can be seen in partial drug resistance. Therefore, when modeling population dynamics where the control of growth and division is phenotype dependent, the corresponding model must take account of the underlying cellular heterogeneity. The finite state projection (FSP) approach has often been used to analyze the statistics of independent cells. Here, we extend the FSP analysis to explore the coupling of cell dynamics and biomolecule dynamics within a population. This extension allows a general framework with which to model the state occupations of a heterogeneous, isogenic population of dividing and expiring cells. The method is demonstrated with a simple model of cell-cycle progression, which we use to explore possible dynamics of drug resistance phenotypes in dividing cells. We use this method to show how stochastic single-cell behaviors affect population level efficacy of drug treatments, and we illustrate how slight modifications to treatment regimens may have dramatic effects on drug efficacy.
R. Johnson and B. Munsky, The finite state projection approach to analyze dynamics of heterogeneous populations, Physical Biology, 14:3, 035002 (2017), online here